標準曲線的回歸分析
發布時間:2017-09-01
一、一元線性回歸方程
在分析化學中,經常使用標準曲線來獲得試樣某組分的濃度。如光度分析中的濃度-吸光度曲線;電位法中的濃度一電位值曲線等。怎樣才能使這些標準曲線描述得最為準確,誤差最小呢?這就需要找出濃度與某特征值兩者之間的定量關系以及代表這種關系的回歸方程。以下簡介回歸方程的計算方法。
設濃度x為自變量,某特征參數了為因變量,在x與y之間存在一定的相關關系,當用實驗數據xi和yi繪圖時,由于測量儀器本身的精度以及測量條件的微小變化等都會給測量帶來誤差,因此用各測量點的測量值繪圖就不可能全部在一條直線上,而是分散在直線的周圍。為了找出一條直線,使各實驗點到直線的距離最短,即誤差最小。需要用數理統計方法,利用最小二乘法計算出相應的方程yi=a+bxi后再繪出相應的直線,這樣的方程稱為y對x的線性回歸方程,相應的直線稱為回歸直線,從回歸方程或回歸直線上求得的數值,誤差小,準確度高。式中的a為直線的截距,與系統誤差大小有關;b為直線的斜率,與方法靈敏度有關。
設實驗點為(xi,yi)(i=1→n),則平均值:

由最小二乘法得:
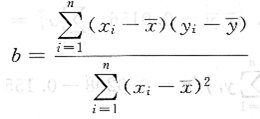
或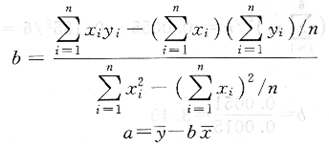
若a、b值確定,回歸方程也就確定了。但這個方程是否有意義,還需要判斷兩個變量x與y之間的相關關系是否達到一定密切程度,因為即使數據誤差很大,仍可以求出一回歸方程。為此可采用相關系數(r)來檢驗。
二、相關系數
相關系數r由下列公式計算:
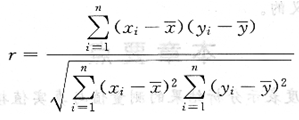
當r=1時,兩變量完全線性相關,實驗點全部在回歸直線上。
R=0時,兩變量毫無相關關系。
0<|r|<1時,兩變量有一定的相關性,只有當|r|大于某臨界值時,二者相關才顯著,所得的回歸方程才有意義。
r的臨界值與置信度及自由度有關,如表所示。如果計算的r大于表上相應數值,則表示所求的回歸直線方程有意義;反之,則無意義。
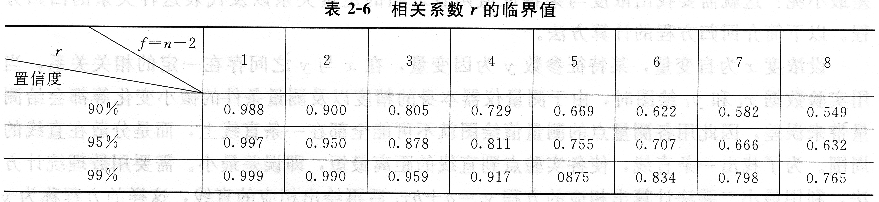
參考資料:分析化學







