首頁>技術中心>技術資訊>少量數據的統計處理――t分布曲線 (一)
少量數據的統計處理――t分布曲線 (一)
發布時間:2017-09-01
態分布是對無限次測量而言的,而在實際工作中,只能對隨機抽得的樣本進行有限次測定。數據處理的任務就是通過對有限次測量數據合理的分析,對總體做出科學的論斷。其中包括對總體平均值的估計和對它的統計檢驗。
對于有限次測定,通常無法知道總體標準偏差σ和總體平均值μ,只能用樣本標準偏差s來估計測量數據的分散情況。用s代替σ,必然引起誤差,從而導致正態分布的偏離,這時可用t分布來代替,以補償這一誤差。t分布是由英國統計學家兼化學家戈塞特(W.S.Gosset)提出的。t的定義與u一致,只是用s代替σ,即:

也可衍生出:
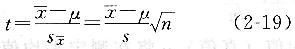
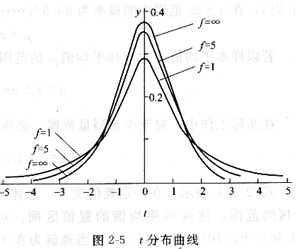
t分布如圖2―5所示,縱坐標同正態分布仍為概率密度y,但橫坐標則將u改為用t表示。由圖可見,t分布曲線與正態分布曲線相似,只是t分布曲線因自由度f的不同而不同。當f>20時,二者很接近,當f→∞時,t分布就趨近正態分布。
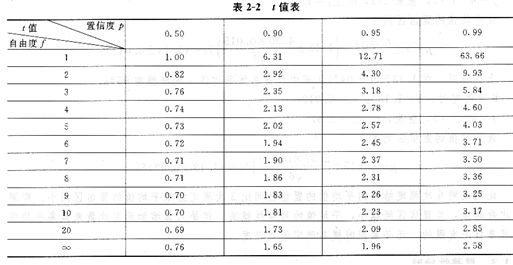
與正態分布曲線一樣,t分布曲線下面某區問的面積,也表示測定值或隨機誤差出現的概率。應該注意,對于正態分布曲線,只要“值一定,相應的概率也就一定;但對于t分布曲線,當t值一定時,由于f值的不同,相應曲線所包圍的面積,即概率卻不同。不同概率及不同廠值所相應的t值已有數學家計算出來,表2-2列出了部分常用的t值。由于t值與置信度及自由度有關,所以通常用ta,f表示。α=1-ρ,根據置信度的定義,α為測定值落在某區間之外的概率,稱為顯著性水平。t0.05,9=2.26表示概率(置信度)為95%,自由度f為9(測定次數n為10)時的t值。
平均值的置信區間:
如前所述,只有當n→∞,x→μ,才能準確地找到總體平均值μ,顯然,實際上是做不到的。從“2.2.2偶然誤差的區間概率”可知,如果用單次測定結果(x)對總體平均值μ的范圍作出估計,則μ包括在x±1ρ范圍內的概率為68.3%,在x±1.96ρ范圍內的概率為95.0%,在x±2ρ范圍內的概率為95.5%……它的數學表達式為:

若以樣本平均值x

在實際工作中,對于少量測量數據,必須根據t分布進行統計處理,按t的定義可得出:

式(2-22)表示:在一定置信度下,總體平均值(真值)μ將在測定平均值x
只要選定置信度,從測定結果的x
置信區問的寬窄與置信度、測定值的精密度、測定次數有關,當測定值的精密度愈高(s愈小)測定次數(n)愈大時,置信區間愈窄,即平均值愈接近真值,平均值愈可靠。
置信度選得愈高,置信區間就愈寬,其區間包括真值的概率也就愈大,在分析化學中,一般選置信度95%或90%。
顯著性檢驗:
在實際工作中,對試樣的分析結果,可能與標準值不同;或者兩種方法、兩個實驗室或兩名分析人員對同一試樣的分析結果會彼此不同,其原因可能是存在著隨機誤差或系統誤差。如果是隨機誤差所致,那么從統計學來說是正常的;但如果是系統誤差所致,那就稱此兩組結果存在顯著性差異。要確定是否存在系統誤差,就要作顯著性檢驗。在定量分析中常用t檢驗法和F檢驗法。
t檢驗法:
(1)平均值與標準值的比較
為了評價某一分析方法或操作過程的可靠性,可將分析數據的平均值與試樣的標準值進行比較,檢驗兩者有無顯著性差異,以確定分析方法是否存在系統誤差。
作t檢驗時,先將標準值μ與平均值x

再根據置信度(通常為95%)和自由度f,由t分布表中查出t值。
若t計算>t表,則說明x
(2)兩組數據平均值的比較
不同分析人員或同一分析人員采用不同方法分析同一試樣,所得的平均值,經常是不完全相等的。為了比較兩組數據是否有顯著性差異,亦可采用t檢驗法。
若兩組測定結果分別為(x

若無顯著性差異,進而用t檢驗法檢驗兩組平均值之間有無顯著性差異。按下式計算t值。
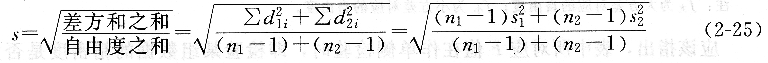
在一定置信度下,查得表值t表(總自由度f=n1+n2―2),若t計>t表,則兩平均值有顯著性差異。若t計<t表,則不存在顯著性差異。
參考資料:分析化學







