測量數據統計學原理及表達(二)
發布時間:2017-09-01
二、數理統計中的基本概念
1、測量誤差及其分類
由測量所得到的被測量值與被測量的真值之間的差叫做測量誤差。測量誤差可以用這個差值來表示,也可以用該差值與被測量的真值之比來表示,所謂被測量的真值是指一個量在被觀測時,該量本身所具有的真實大小。由于被測量的真值一般來說是不知道的,所以選擇真值的最佳估計值以及確定該估計值的誤差就是數據處理中的首要問題。
按照誤差的性質及產生的原因,通常可將誤差分為三類:偶然誤差(或隨機誤差)、系統誤差和疏失誤差。
假定對一個量作n次測量,測得數據為:

偶然誤差是指在實際測量條件下,多次測量同一量時,誤差的絕對值和符號以不可預定方式變化著的誤差。當測定次數足夠多時,出現數值相等、符號相反的偏差的概率近乎相等,各種大小偏差出現的概率遵循著統計分布規律。例如,遵從正態分布的誤差具有以下幾個特點:
(1)單峰性:絕對值小的誤差出現的概率比絕對值大的誤差出現的概率大;
(2)對稱性:絕對值相等的正誤差和負誤差,其出現的概率相等;
(3)有界性:絕對值很大的誤差出現的概率近于零,亦即誤差有一定的實際限度;
(4)抵償性:在實際測量條件下對同一量的測量,其誤差的算術平均值隨著測量次數增加亦趨于零。
引起偶然誤差的因素是無法控制的。雖然不能找到適當的因數對偶然誤差予以校正,但可以通過增加測定次數在某種程度上將它減小。
系統誤差是指在同一條件下多次測量同一量時,誤差的絕對值和符號保持恒定,或在條件改變時,按某一確定的規律變化的誤差。對于那些絕對值和符號保持恒定的已定系統誤差,可以按照它作用的規律,對它進行校正或設法消除它。對那些不能確定的但其值又足夠大的系統誤差,在計算測量的總誤差時予以估計并和其他誤差進行合成。企圖增加測量次數是不能使系統誤差減小的。
疏失誤差是指那些超出在規定條件下預期的誤差,是一種顯然與事實不符的誤差,主要是由于工作人員的疏忽或測量儀器的不正確使用所造成的。這是在測量過程中應避免的一類誤差。
反映系統誤差的大小常用“正確度”一詞;反映偶然誤差的大小常用“精密度”一詞。圖2―1說明它們之間的區別。
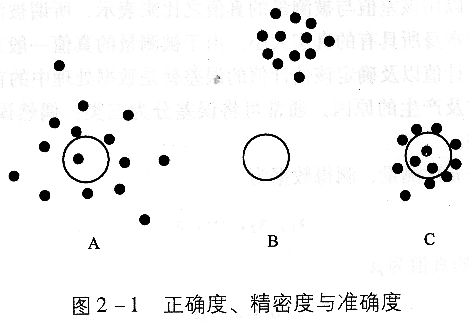
圖2―1中A表示系統誤差小,而偶然誤差大,即正確度高而精密度低;B表示系統誤差大,而偶然誤差小,即正確度低而精密度高;C表示系統誤差與偶然誤差均小,即準確度高。
應該注意到,由于被測量的真值在絕大多數情況是未知的,因此誤差應該理解為是一個定性的概念,而不應該理解為是一個定量的概念,所以嚴格說來誤差只能說高低、大小,而不應表達為諸如0.1或l%等。
2、表示一組數據集中位置的特征數
假設一個分析工作者用某一分析方法對標準物質的某一特性做出一組等精度測量,測得數據為:xl,x2,…,xn。
(1)算術平均值x-:

(3)中位數M
將觀測值按由小到大的順序排列,屬于中間位置的測量值稱為中位數(若測量個數為偶數,則為居中的相鄰兩數的平均值)。
(4)眾數M0
在數值的頻數分布表中,使頻數達到最大值的那個數值即為眾數。
(5)均方根平均值u

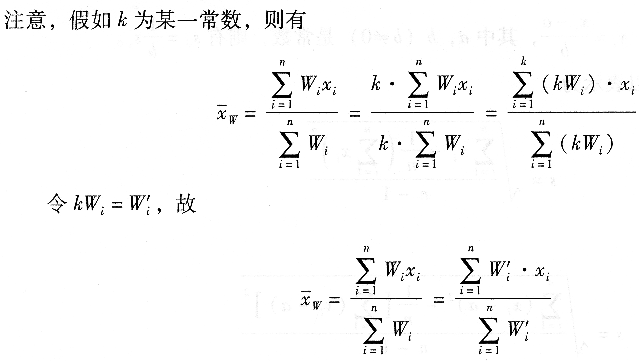
也就是說權同時乘一個常數對加權平均值并無影響。
另外,假若一個加權平均值的權均相同,即Wi=W,則有:
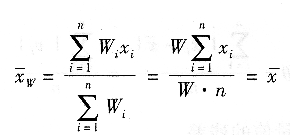
也就是說當權完全相同時,加權平均值和算術平均完全相同,即算術平均值是加權平均值權完全相同的一種特例。
(7)調和平均數H
![]()
按照數理統計理論,測量值在服從正態分布情況下,可以證明算術平均值x-為測量結果的最佳值。它是最常用的表示集中位置的特征數,因此通常都是用算術平均值來表示測定結果。
參考資料:標準物質定值原則和統計學原理







