測量數據統計學原理及表達(三)
發布時間:2017-09-01
3、表示一組數據離散程度的特征數
(1)標準偏差s
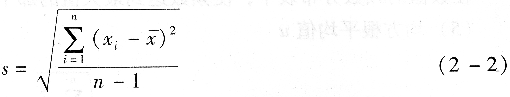

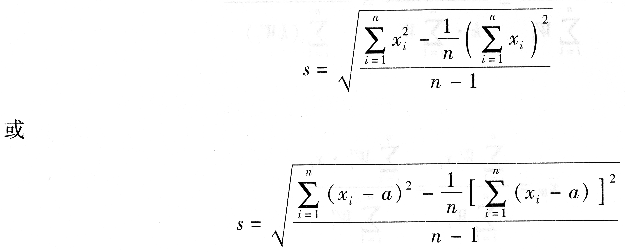
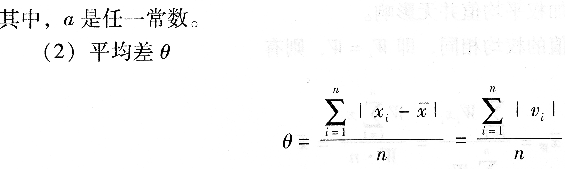
其中,vi=xi一x-稱為第i個測量值的殘差。
(3)極差R
極差是指一組觀測值中最大值和最小值之差。
(4)或然誤差ρ
或然誤差是指在一組測量值的誤差中,落在-ρ到+ρ范圍內的誤差個數與落在該區間之外的誤差個數相等,或者說在所有的測量誤差中,有一種誤差,比它大的與比它小的誤差的出現可能性恰好相等,這一誤差就叫或然誤差。
在數理統計中,用方差σ2來評價測量值與真值的偏離程度,若以μ表示被測量的真值,則有:
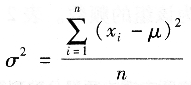
可以證明s2是σ2的無偏估計。由于標準偏差不僅是一組測量中各個觀測值的函數,而且對一組測量中的較大誤差感覺比較靈敏,故標準偏差為表示精度的較好方法。
若兩組測量的殘差分別為:

即按平均差表示兩組數據離散程度相同。
但若按標準偏差表示:
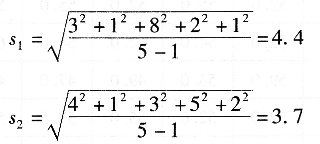
由此可見,第一組中比較突出的大誤差在標準偏差中就可以較好地反映出來。
用極差表示的缺點是它僅取決于兩極端值,而與測量次數無關,因此它所使用的一組數據的信息就少得多。
根據或然率理論,當測量次數相當大時,則有如下關系:
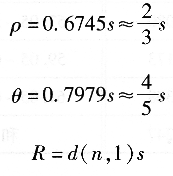
在正態分布時,d(n,1)值可由表2―5中查出。

在通常情況下,計算s時,采用式(2―2)為最好。該式亦稱為貝塞爾(Bessel)公式。
4、正態分布及其檢驗
如將一個量的測量結果按由小到大的順序排列,并按照一定的問隔將其分成若干組時,則每一組中測量數據的數目稱為該組的頻數。表2―6、表2―7列出某物質中銅含量分析結果及其分布。
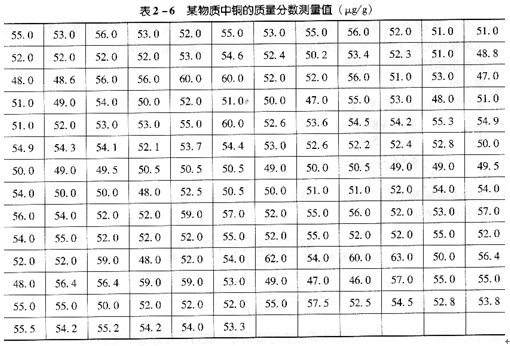
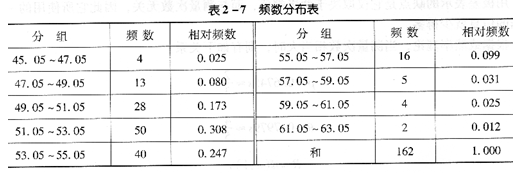
從表2―7中可以看出測量值的波動規律。為更直觀起見,以橫坐標表示測量值的大小,標出分組的點;以縱坐標表示頻數,畫出一個個矩形,這個圖稱為頻數分布直方圖(見圖2―2)。頻數與總的測定次數之比稱為相對頻數,同樣可以作出相對頻數分布直方圖(見圖2―3)。
參考資料:標準物質定值原則和統計學原理







