測量數據統計學原理及表達(九)
發布時間:2017-09-01
在計算A類不確定度時應注意單次測量不確定度與測量列算術平均值不確定度的區別。
作為測量列中單次測量的不確定度可表示為U(x)=ta(n-1)s,這里ta(n-1)為與顯著性水平α以及測量次數凡有關的因子,稱為t分布的臨界值或t分布的分位數,其值列于表2-18中。當測量為正態分布,且測量次數足夠多時,對置信概率為99%(即顯著性水平為1%),可取t=2.58,即單次測量的不確定度為2.58s。對置信概率為95%(即顯著性水平為5%),可取t=1.96,即單次測量的不確定度為1.96s。
作為測量列算術平均值的不確定度可表示為![]() 其中n為測量次數。
其中n為測量次數。
(2)不確定度來源
化學分析測量不確定度的來源有以下幾種:
①被測對象的定義不完善,例如被測定的物質缺少確切的結構說明。
②取樣帶來的不確定度,測定樣品可能不完全代表所定義的被測對象。
③被測對象的預富集和分離的不完全。
④基體影響和干擾。
⑤在抽樣、樣品制備、樣品分析過程中的沾污,這對痕量分析工作尤為重要。
⑥在對環境條件的影響缺乏認識或環境條件的測量不夠完善,例如容量玻璃器具校準與使用時溫度不同所帶來的不確定度。
⑦讀數不準,讀取計數或刻度形成的習慣性偏高或偏低傾向
⑧稱量和容量儀器等的不確定度。
⑨儀器的分辨率、靈敏度、穩定性、噪聲水平、儀器的偏倚、檢定校準中的不確定度以及自動分析儀器的滯后影響等。
⑩測量標準和標準物質所給定的不確定度值,特別是作為基準或標準用的試劑純度的影響。有機純物質由于同分異構體和無機鹽的存在,在配制標準溶液時應考慮純度這一重要因素。
(11)從外部取得并用于數據的整理換算的常數或其他參數的值所具有的不確定度。
(12)包括在測量方法和過程中某些近似和假設,某些不恰當的校準模式選擇。例如使用一條直線校準一條彎曲的響應曲線,數據計算中舍、人影響。
(13)測量過程中的隨機影響對不確定度的貢獻。
所有這些影響不確定度的因素對總不確定度的貢獻要做全面的分析評定,但有時這些因素之間并不一定都是獨立的,所以必須考慮相互之間的影響對不確定度的貢獻,即要考慮協方差。
(三)不確定度估計方式
①測量的數學模型建立對測量過程的全面了解。要了解測量是如何進行的,弄清被測量及其參數之間的關系,要對已知的系統性影響進行修正。由于大多數化學測量結果是在程序最終才獲得的.因此要對中間量進行仔細研究,還需注意使用的常數。如果被測對象和其他量有函數關系
y= f(x1,x2,…,xn)
則這個關系的建立對評價被測對象的不確定度是重要的。要通過對x1,x2,…,xn等每一個量的不確定度給出y的不確定度。如果函數關系沒有建立起來,就需要從實驗或其他方式估計這些量對被測對象的影響,最終合成給出被漢0對象的不確定度。
②鑒別不確定度來源(見前述)并量化不確定度分量要對每一個不確定度來源通過測量或估計進行量化。實際上最大分量的1/3的那些分量是不用估計的,因此量化的第一步是要預先估計每一個分量對合成不確定度的貢獻,排除那些不太重要的分量,這樣就簡化了不確定度分量的列表。
在很多情況下,不確定度分量隨分析物的含量水平而變化。因此,確定不確定度程序應有所限制,即應在分析物含量水平附近的一個小范圍內進行不確定度評估,或者給出含量水平與不確定度的相關性,然后計算出分析物含量水平下的不確定度。
對不確定度分量的量化可采用下述四種方式:
a.通過實驗進行定量。
b.使用標準物質進行定量,此時需要考慮標準物質作為計量標準,其量值本身也有不確定度;在標準物質上所進行的測量的再現性;對標準物質測量所得測量值與該標準物質所具有的標準值之間的差異;標準物質成分和被分析樣品成分之間的差異;測量系統對標準物質和被分析樣品適應性的差異;取樣所具有的不確定度。
c.基于以前的結果或數據的估計進行定量,包括來自供應商的信息、實驗室之間的研究,熟練實驗的結果、質量保證數據。
d.基于判斷進行定量。

當誤差限是由證書或其他說明書中得到,且沒有明確給出確定的置信水平;當估計的誤差限是以最大范圍形式給出的,且沒有對該誤差的分布狀況方面的知識時;當誤差的性質偏重于系統性的誤差時,建議按均勻分布處理。
當誤差的性質偏重于隨機性的,雖沒有指定分布形式,但給出標準偏差或相對標準偏差(RSD)時;明確給出確定的置信水平的不確定度或置信區間,但沒有指明分布,此時建議作為正態分布處理。 ③合成標準不確定度的計算
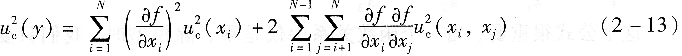
式中:uc(y)――y的標準不確定度;
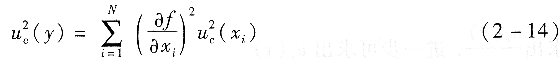
參考資料:標準物質定值原則和統計學原理







