實驗數據處理分析測試的特點(一)
發布時間:2017-09-01
分析測試是一個獲取分析對象化學組成和結構信息的過程,為工農業生產、國內外貿易、科技發展和社會進步提供大量準確可靠的分析檢測數據,作為正確評價科技成果、保證工農業生產和國內外貿易正常進行的基礎技術資料。為了獲得準確可靠的分析檢測數據,必須了解整個分析測試與從分析測試數據提取信息的過程及其特點。化學分析和大多數儀器分析的特點大致可以歸結為:分析過程具有復雜性;分析測試數據具有統計波動性;抽樣檢驗是基本的分析測試方式。
與物理測量相比,化學分析和大多數儀器分析過程都比較復雜,包括采樣、樣品前處理如溶(熔)解、消化、分離或富集、測試等多個相互聯系的環節,分析測試結果受到多種因素的影響,涉及抽樣的代表性和來自基體的影響;可能發生的樣品損失、沾污;樣品制備和測量方法引入的人為操作、測試方法和儀器誤差等。分析測試過程中任何一個環節的失誤,都將對測試結果產生重要影響,甚至導致一次測試的完全失敗。
由于分析測試過程的復雜性與影響因素多,而各因素的影響又難以完全控制,從而導致在同樣條件下測得的數據參差不齊,有時表面看起來似乎有點“雜亂無章”。從測定誤差的角度考慮,測定量值是一個以概率取值的隨機變量,不可避免地要受到隨機誤差的影響,有時又要受到系統誤差的影響,使得測定量值具有統計波動性。分析人員若不采用科學的方法去分析和處理這些參差不齊、表面看來似乎是“雜亂無章”的測試數據,就無法發現寓于其中的統計規律性,進而引出符合客觀實際的科學結論。由此可見,數據統計處理是整個分析測試過程不可分割的一部分。
在相當多的情況下,被分析的原樣品不能直接上機測定,需要對原樣品進行預處理,將原樣品轉變為適合于某種分析儀器測定的試驗樣品(試樣)。這就是說,被分析原樣品在上機測定之前已受到破壞,原樣品分析完之后不復存在,通過分析測試數據對直接測定的試樣本身做出結論已經沒有什么實際意義。測試樣品的目的只是通過測試樣本(試樣),獲得有關樣本(試樣)的信息,由樣本信息以一定的置信度去推斷和估計測試樣本(試樣)所來自的總體(原樣品)的特性。比如用原子吸收光譜法檢查一批出El豬肉罐頭的含鉛量,當測得豬肉罐頭的鉛含量之后,作為直接測定試樣的豬肉罐頭已受到破壞,已不能再作為商品出售。測定其中含鉛量的目的,是從它的含鉛量去估計和推斷“罐頭樣品”抽樣的那一批出口豬肉罐頭的含鉛量是否合格。由于儀器分析在大多數情況下是“破壞性”分析,決定了儀器分析采用的基本方式是抽樣檢驗。
由于儀器分析采用的基本方式是抽樣檢驗,要通過對試樣的測試去了解和獲得有關分析總體(原樣品)的定性、定量、形態和結構等方面的信息,對原樣品的品質屬性做出科學的結論。要做到這一點,至少要解決3個基本問題:①所抽取的樣本對總體有足夠的代表性,為此要采用科學合理的方法抽樣和取樣;
②對樣本的分析測試結果(數據、圖譜等)是可靠的,為此要求在整個分析測試過程中實施嚴格的質量控制;③由樣本信息推斷總體特性時,必須遵循科學的推理方法。這3個基本問題的解決都離不開分析檢測數據的科學處理。
一、分析測試數據統計處理基礎
在分析測試中,測定量值是一個以概率取值的隨機變量。而在大量重復試驗中得到的測定量值具有統計規律性,測定量值的概事分布遵循正態分布,其期望值為E(χ)=μ,方差為D(χ)=σ2。正態分布的概率密度函數為:
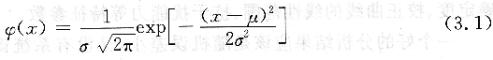
記為N(μ,σ2)。由式(3.1)可以看到,當μ和σ已知,概率分布就完全確定了,給定任一的χ值,就可以確定該χ值出現的概率。這就是說,全部測定量值的概率分布可以用岸和口兩個基本參數來表征它。μ確定了概率分布中心在χ軸上的位置,表征測定量值的集中趨勢,σ表示測定量值沿χ軸的散布,表征測定量值的離散特性。正態分布是大量觀測所得到的測定量值的理論分布曲線,但在實用上,當測定量值數目大于30時,通常可用正態分布近似描述測定量值和測量誤差的分布特性。在有限次測定中,人們不可能獲得總體的平均值肚和標準偏差σ,但可以得到樣本的平均值χ和樣本的標準偏差s。如果樣本平均值χ和樣本標準偏差s能夠充分近似地代表總體平均值μ和總體標準偏差一,那就可以用樣本平均值z和樣本標準偏差s來表征全部測定量值的分布特性。
現在的問題是χ和s是否能充分近似地代表μ和σ。數理統計理論已經證明:在等精度測量中,樣本平均值χ是一組測定值中出現概率最大的值,是μ的無偏估計值和具有最小方差的最優估計值,樣本方差s2是σ2的無偏估計值,用χ和s來分別代表參數μ、σ時沒有系統誤差;在不等精度測量中,樣本加權平均值χ。是一組測定值中出現概率最大的值,是μ的無偏估計值和具有最小方差的最優估計值,樣本加權平均值標準偏差sW是σ的無偏估計值。因為樣本平均值χ和樣本標準偏差s能夠充分近似地代表總體平均值“和總體標準偏差一,所以,在分析測試中,常用樣本平均值和樣本標準偏差來報告分析檢測結果。
前面曾經指出,測定量值具有統計波動性。在正常的情況下,測定量值統計波動的程度應該是多大?按照數理統計理論,各個測定量值出現的概率遵循正態分布,由式(3.1)可以計算測定量值落在2倍標準偏差之外的概率小于5%,落在3倍標準偏差之外的概率小于0.3%。由2倍標準偏差或3倍標準偏差所構建的區間,即是分析測試中所允許的合理誤差范圍。這個合理誤差范圍為分析人員判斷和取舍分析數據、評價數據的可靠性與分析結果溯源提供了理論依據。
二、評價分析方法和分析結果的基本指標
一個好的分析方法應具有良好的檢測能力,易獲得可靠的測定結果,有廣泛的適用性。此外,操作應盡可能簡便。檢測能力用檢出限表示,測定結果的可靠性用不確定度表示,適用性用校正曲線的線性范圍和抗干擾能力來衡量。因此,在評價分析方法時,應給出方法的檢出限、用該法測定某一或某些特定成分的不確定度、校正曲線的線性范圍、抗干擾能力等特征參數。
一個好的分析結果應該是隨機誤差小,又沒有系統誤差。隨機誤差影響測定結果的精密度,用標準偏差或相對標準偏差表征。系統誤差影響測定結果的準確度,用誤差或相對誤差表征。獲得一個同等精密度和準確度的分析結果,對不同的分析人員所花費的勞動是有差異的,所花費的代價用測定次數表征。因此,為了科學地評價一個分析結果,在報告分析結果時,應該給出測定平均值、標準偏差、誤差(在不存在系統誤差時不給出)和測定次數等基本參數。
1、檢出限和靈敏度
檢出限是指能產生一個確證在試樣中存在被測組分的分析信號所需要的該組分的最小含量或最小濃度。在測定誤差遵從正態分布的條件下,指能用該分析方法以適當置信度(通常取置信度99.7%)檢出被測組分的最小量或最小濃度。最小檢出量和最小檢出濃度可由最小檢測信號值與空白噪聲導出,分別以qL和cL表示:

參考資料:現代儀器分析實驗與技術







