鐵磁共振參數標準樣品的研制
發布時間:2017-09-01
微波鐵磁器件廣泛應用于雷達、通信、導航、電子對抗、導彈制導、航空航天、深空探測及精密測量等系統中,是現代微波電子設備不可缺少的基本元器件,這些應用中的關鍵參數是共振參數,共振參數的準確測量決定了這些應用質量。遺憾的是共振參數的量值溯源一直未能解決。
筆者提出了采用鐵磁標準樣品建立量值溯源的方案,經小范圍運作,效果良好,共振線寬擴展測量不確定度小于20%,可滿足科研和生產需要。課題的關鍵技術之一是研制一套性能穩定、線寬重復性好、覆蓋范圍為(0.25~6.28)A/m的鐵磁標樣。
一、鐵磁共振理論
鐵磁物質的磁性來源于原子磁矩。鐵磁性物質中電子的自旋交換作用形成磁有序,其內部形成許多磁矩取向一致的微小自發磁化區(俗稱“磁疇”)。平時“磁疇”的排列方向是混亂的,所以對外不顯磁性。在足夠強的外磁場作用下,“磁疇”的排列方向有序,顯示出磁性。某些鐵磁材料在直流磁場和微波電磁場的共同作用下顯示出明顯的鐵磁共振現象,這在微波領域有重要應用。處于穩恒磁場和微波磁場H中的鐵磁物質,它的微波磁感應強度B可表示為
B=μ0μijH(1)
式中:μij――張量磁導率;μ0――真空中的磁導率。
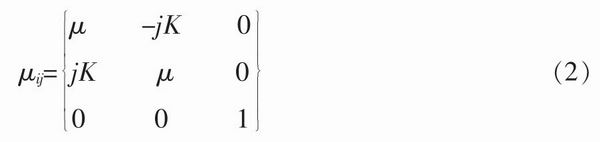
式中:μ、K――張量磁導率的元素。其中,μ為對角分量,K為反對角分量,用公式表示如下:
μ=μ′-jμ″ (3)
K=K′-jK″ (4)
μ、K的實部和虛部隨B的變化曲線如圖1(a)、1(b)所示。
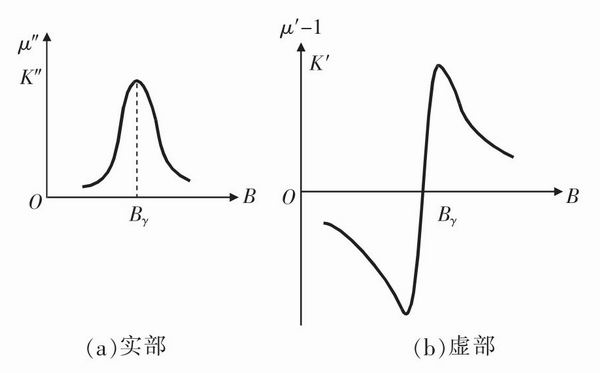
<CTSM> 圖1 變化曲線</CTSM>
μ′、K′在Bγ=ω0/γ處的數值和符號都劇烈變化,稱為色散。此時,μ″、K′達到極大值,稱為共振吸收,此現象即為鐵磁共振。這里ω0為微波磁場的旋轉頻率,γ為鐵磁物質的旋磁比。

式中:μB=he/2me=9.2741×10-24J?T-1,稱為玻爾磁子;h=6.6262×10-34J?s,是普朗克常數;g為朗德因子(度量軌道磁矩和自旋磁矩相對于總磁矩的貢獻)。
μ″定義為鐵磁物質能的損耗,鐵磁材料在頻率為f0的微波磁場中,且加在鐵磁材料樣品上的穩恒磁場滿足Bγ=B0=ω0/γ時,磁損耗最大。常用共振吸收線寬ΔB來描述鐵磁物質的磁損耗大小。ΔB定義為μ″=0.5μm處對應的磁場間隔(B2-B1),即半高度寬度,如圖2所示。
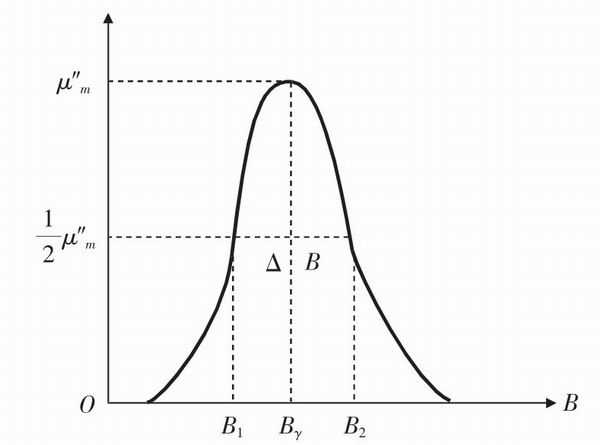
<CTSM> 圖2 共振吸收線寬ΔB定義圖</CTSM>
二、鐵磁薄膜的磁損耗機理
鐵磁薄膜在GHz頻段的剩余損耗主要是自然共振損耗,在磁損耗中占很大的比重。
鐵磁薄膜的磁損耗分為本征損耗和非本征損耗兩類。本征損耗(也稱Gilbert損耗)來源于物質最基本的性質,例如自旋軌道相互耦合作用、磁結構或晶格等;非本征損耗主要來源于樣品內部的不均勻性。本征損耗是系統不可分割的一部分,來源于不可避免的因素,是不可被抑制的。而非本征損耗來源于物質的微觀結構缺陷,強烈依賴于薄膜制備工藝,因此是可以被改變的。通過調整鐵磁的各種損耗,可以獲得需要的共振線寬值,滿足鐵磁標樣覆蓋范圍的需要。
1.本征損耗
本征損耗來源于自旋-軌道耦合作用和自旋反轉。微波電磁場的一致進動能量,通過自旋-軌道耦合和載流子直接傳遞給晶格,稱為本征散射過程,如圖3所示。對于金屬薄膜的Gilbert損耗,最重要的貢獻是通過磁子和聲子由巡游傳導電子的不連續散射引起的。
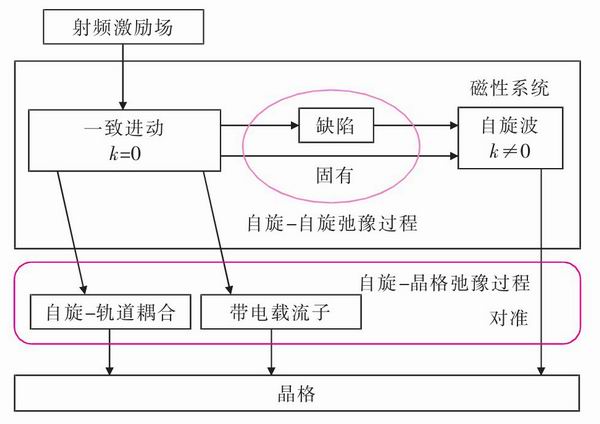
<CTSM> 圖3 薄膜損耗機制示意圖</CTSM>
另一個過程發生在鐵磁性金屬中。當磁化方向被改變時,費米面的形狀也發生變化,因此,由于自旋軌道耦合的作用,一致進動將導致費米面周期性的變化。對于自旋-軌道耦合導致的弛豫,其阻尼系數a(GHz-1?S-1)的微觀表達式為

式中:γ――鐵磁物質的旋磁比,A/m-1?s-1;Ms――飽和磁化強度,emu/cm3;EF――費米能級,emu;g――朗德因子;τ――軌道弛豫時間,s;λ――自旋-軌道耦合系數。
從Gilbert本征損耗阻尼系數的微觀表達式可以看出,對于金屬中的阻尼自旋-軌道耦合是非常重要的,因為朗德因子取決于自旋角動量和軌道角動量的比值。所以,由此看出Gilbert損耗是物質本身的內稟屬性,與磁結構或晶格等本身性質有關。由Gilbert本征損耗導致的線寬在磁譜和鐵磁共振曲線上與微波頻率呈線性關系,與樣品的質量和外加磁場的大小沒有直接關系。
2.非本征損耗
非本征損耗是指鐵磁性物質中除了本征損耗外其他所有的磁損耗機制,主要有雙磁子散射和非均勻散射。如圖3所示,在雙磁子散射過程中,具有波矢k=0的一致進動磁子被湮滅,然后產生一個k≠0的磁子,由于這是一個自旋-自旋弛豫過程,所以總的磁子數量沒有改變。然而對于k≠0的磁子自旋不再互相平行,自旋一致進動通過這個過程將能量傳遞給自旋波,最終k≠0的自旋波將得到的能量轉移到晶格。例如雜質、空洞、孔隙、非磁性相等,從一致進動到自旋波的散射才能產生,它們導致材料內部的電子自旋在微波場的微擾下無法保持一致進動,偏移原來的有序排列狀態。
非本征損耗除了雙磁子散射外,還有很多不均勻因素,如多磁相結構和不均勻性造成的彌散、顆粒尺寸的大小分布和界面與表面的粗糙度等也會產生散射作用,從而導致自旋波的衰減。在有些情況下這一部分的貢獻要比Gilbert本征損耗大1~2個數量級,甚至還有可能超過雙磁子散射的貢獻。一般情況下,從鐵磁共振和磁譜虛部共振峰的形狀來看,Gilbert本征損耗和雙磁子散射導致的共振峰曲線為洛倫茲型,而非均勻散射為高斯型,所以可以從形狀上做一定的區分。
三、材料的選擇與鐵磁共振線寬的調整方法
由LLG方程和鐵磁共振線寬的定義,可以得到對掃場模式的測量,其線寬與阻尼系數α的關系為

式中:ΔH――共振線寬,A/m;ΔH0――本征線寬,A/m;α――阻尼系數,GHz-1?s-1;f――微波頻率,GHz;γ――鐵磁物質的旋磁比,A/m-1?s-1。
從式(7)看出要改變共振線寬,就只能改變非本征線寬。測試頻率是規定了的,對于確定的合金材料,γ系數也基本不變,只有通過改變阻尼系數才能改變線寬。標樣的基本材料選用的是NiFe合金,通過以下方法來改變材料的阻尼系數。
1.改變材料配比獲得不同阻尼系數
以Ni1-xFex合金薄膜為例說明。由于Fe的磁晶各向異性常數K1=+48.1×103J/m3,而Ni的磁晶各向異性常數K1=-5.48×103J/m3。通過適當的配比,比如x=20%左右,就可以獲得磁晶各向異性常數接近于零的優異磁性材料,這就是工業界應用廣泛的坡莫合金的配比。
在坡莫合金中,由于合金的有效磁晶各向異性接近于零,材料呈現各向同性,在良好的工藝情況下,坡莫合金呈現完美的立方結構,材料中不存在非本征的雙磁子散射和非均勻散射,故而阻尼系數小,如圖4所示。
隨著Fe含量的增大,合金薄膜材料的磁晶各向異性常數越來越大,其非本征的雙磁子散射和非均勻散射增加,阻尼系數越大,線寬也就越大,圖4是試驗結果,x為Fe在NiFe合金中的含量比。
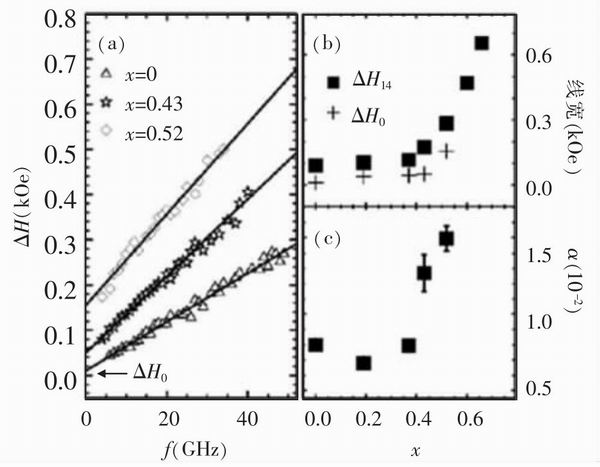
<CTSM> 圖4 Ni1-xFex的鐵磁共振線寬和阻尼系數與x的關系</CTSM>
2.氧摻雜量可以改變阻尼系數
對NiFe合金薄膜,如果在濺射時通入適當的氧氣,成膜成分為NiFe+(NiFe)1-xOX的混合物。混合物是兩相磁性材料,這兩相的共振峰靠得較近,因此共振線寬被拓寬。另外隨著氧含量的增加,在材料中也會引入較多的缺陷,增加非本征雙磁子散射和非均勻散射,線寬也就越大。較大的線寬所需的外磁場越強,即諧振點的磁場強度也就越大(見圖5)。通過摻雜,可以獲得大的諧振點和大的線寬。
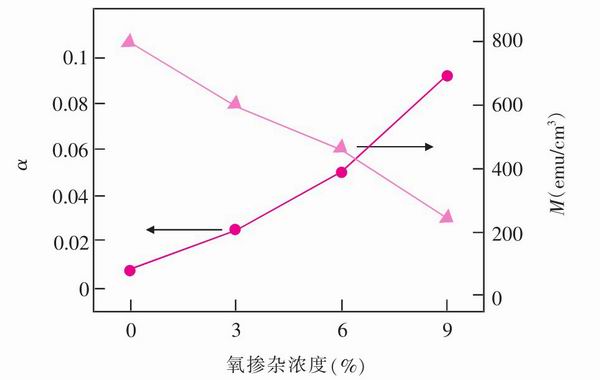
<CTSM> 圖5 NiFe氧摻雜量與阻尼系數和磁化強度的關系</CTSM>
3.利用底層形貌與自旋泵浦效應結合改變共振線寬
利用超高真空磁控濺射制備Ni81Fe19/CuNx異質薄膜,改變氮氣分壓從0到20%制備不同的氮化銅薄膜。測試結果表明,覆蓋不同氮氣分壓沉積的氮化銅的Ni81Fe19/CuNx體系飽和磁化強度和矯頑力等靜態磁參數并沒有區別,然而,覆蓋不同氮氣分壓下CuNx薄膜對鐵磁共振線寬和阻尼因子有顯著影響,基于底層形貌和自旋泵浦模型可對磁阻尼系數的變化趨勢進行合理解釋。圖6是試驗結果。
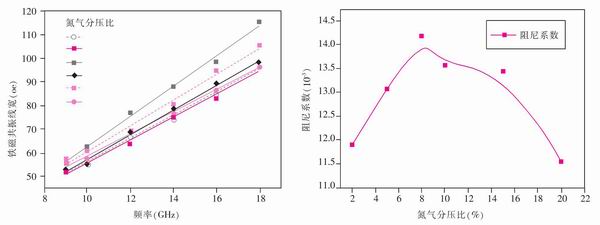
<CTSM> 圖6 底層形貌與自旋泵浦效應結合改變NiFe合金的阻尼系數</CTSM>
四、鐵磁薄膜樣品的制備
根據理論分析結果,筆者設計并制備了多種鐵磁樣品,經測量后修改配比、氧摻雜和形貌再次制作。經過多次的設計-制備-測量-修改的循環,最終研制出一批線寬范圍為(0.125~6.28)A/m的樣品。經高溫老化及反復磁化穩定后,得到一批合乎要求的鐵磁共振參數標準樣片。
五、實驗數據
由于鐵磁材料存在磁滯效應,掃場測量時的掃場測量范圍對共振點和共振線寬影響較大。為了保證樣片共振參數的一致性,嚴格給定樣品的測試頻率、掃場范圍和擬合分析磁場范圍,而且必須從高到低進行掃場。
按規定的測試條件和分析磁場范圍,實驗室1(Lab1)對樣品的線寬進行重復性試驗。實驗每天進行一組,每組重復10次。共進行5組(5天)實驗,每組實驗都重新裝卸樣品,并于系統校準后進行測量,以考核實際量值傳遞過程的重復性。實驗結果見表1的“uA”欄,顯然uA小于標準樣品允差(±20%)的1/3,滿足標樣要求的重復性。uA值采用合并樣本標準偏差sp估算,即
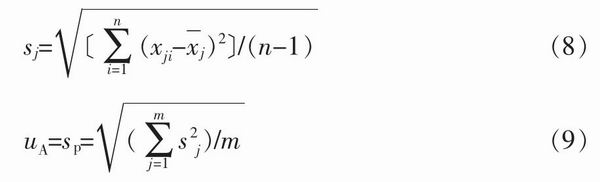
式中:sj――第j組的10次重復測量標準偏差;xji――第j組的i次測量數據;――第j組的10次測量平均值;n――組內重復測量次數,10;uA――用A類評定方法獲得的不確定度分量;sp――共5組、每組10次重復測量的合并樣本標準偏差;m――試驗組數。
兩個實驗室對同一套樣品進行測試,以考核實驗室的測試能力。測試方法與實驗室1相同,其結果平均值的差異見表1“差異”欄。顯然,實驗室間的差異值小于樣品允差,表明實驗室的測試系統符合要求,樣品的變動性也符合要求。
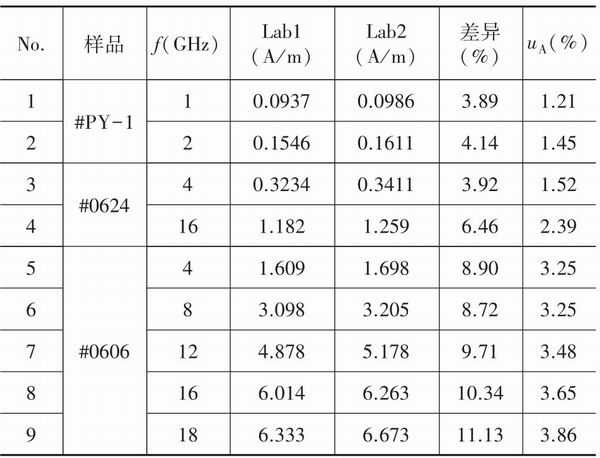
<CTSM> 表1 線寬測試結果</CTSM>
六、均勻性檢驗
依據JJF1006-1994《一級標準物質技術規范》有關均勻性檢驗的指引,采用F檢驗法進行均勻性檢驗。F值的計算公式如下:
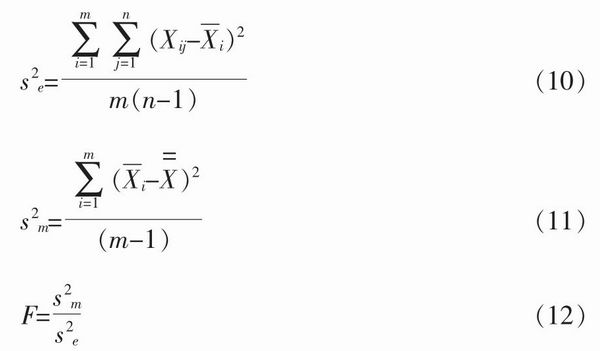
式中:――單元內方差;――單元間方差;n――每單元重復測量次數;m――檢驗抽取單元數;Xij――第i單元的第j次測量;――第i單元的n次測量平均值;Xi――全部m個單元的n次測量總平均值。
本文選用置信概率為95%(a=0.05)作為檢驗判據,則當檢驗結果F≤F〔a,(m-1),m(n-1)〕時,單元間方差與單元內方差無顯著性差異,樣品均勻;否則不均勻。
被檢驗樣片為筆者于2012年6月6日制備的60mm×60mm、厚2mm的大樣片(編號#0606),裁剪成4mm×4mm的225個小片中抽取的10個小片(單元),編號為S1~S10。每個小片(單元)測量5次,按F檢驗法判斷樣片的均勻性。檢驗結論為“均勻”,如表2所示。
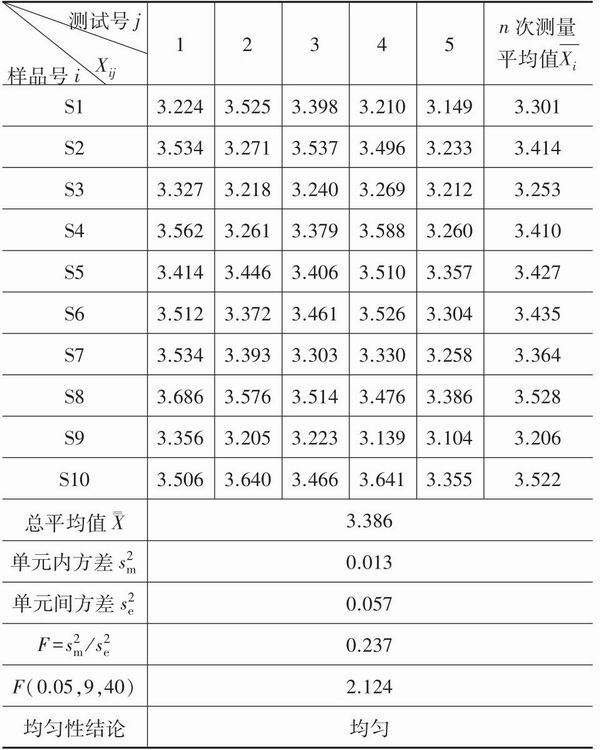
<CTSM> 表 2#0606號樣片均勻性檢驗結果</CTSM>
七、結束語
筆者提出的用標準鐵磁樣片作為標準物質通過共振線寬進行量值傳遞的方法,經理論與實驗證實傳遞的不確定度達到科研和生產的需要,具有較好的應用前景。







