首頁>技術中心>技術資訊>論《方箱檢定規程》中的測量不確定度評定問題
論《方箱檢定規程》中的測量不確定度評定問題
發布時間：2017-09-01
一、模擬式儀表的估讀誤差分析問題
在JJG194-2007《方箱檢定規程》“A.3.2測微表估讀誤差引起的標準不確定度分量u(ai2)的評定”中有:“由于測微表的分度值為1μm，所以其估讀誤差可認為是0.5μm，半寬為0.25μm。……測微表估讀誤差引起的標準不確定度u(ai2)為:u(ai2)=0.25/2=0.12μm”。
筆者認為模擬式儀表的估讀誤差分析，可以參考數字顯示器的分辨力誤差分析方法。JJG194-2007中此處的標準不確定度分析方法是有問題的，有案可稽的是以下權威的模式:在JJF1059.1-2012《測量不確定度評定與表示》的4.3.3.4條款【注】之f)的注5的例中有:“若數字顯示器的分辨力為δx，由分辨力導致的標準不確定度分量u(x)采用B類評定，則區間半寬度為a=δx/2，假設可能值在區間內為均勻分布，查表得k=，因此由分辨力導致的標準不確定度分量u(x)為: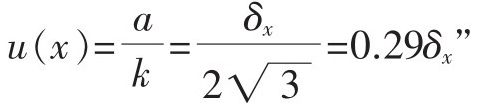
。即:假如數字顯示器的分辨力為δx=1μm，則由分辨力導致的標準不確定度u(x)=0.29μm。同為1μm分辨力的模擬式儀表的估讀誤差引起的標準不確定度不可能小于之。
【注】JJG194-2007適時對應的是JJF1059-1999版的5.9條款:“對于數字顯示式測量儀器，如其分辨力為δx，則由此帶來的標準不確定度為:u(x)=0.29δx”。
二、合成不確定度中某些分量的取、舍與合理性問題
在“A.3輸入量ai的標準不確定度u(ai)的評定”中有:“觀察值ai的不確定度來源主要有:①測微表示值誤差引起的標準不確定度分量u(ai1)；②測微表的估讀誤差引起的標準不確定度分量u(ai2)；③平板平面度引起的標準不確定度分量u(ai3)；④圓柱直線度誤差引起的標準不確定度分量u(ai4)”。
在JJG194-2007的測量不確定度評定分析中，缺少一個極其重要的組成部分/分量，即A類評定中的重復性測量誤差。當然該分量并非缺之不可，但前提是要作如下比較，才能理性地決定取舍。根據JJF1033-2008《計量標準考核規范》附錄C.1.4中的表述:“被測儀器的分辨力也會對重復性測量有影響。在不確定度評定中，當重復性引入的不確定度分量大于被測儀器的分辨力所引入的不確定度分量時，可以不考慮分辨力所引入的不確定度分量。當重復性引入的不確定度分量小于被測儀器的分辨力所引入的不確定度分量時，應該用分辨力引入的不確定度分量代替重復性分量。”
JJG194-2007的附錄A名曰“方箱垂直度測量結果不確定度評定”，卻自始至終對“測量結果”避而不談，直接以4個分量中最小、完全可忽略不計的0.12μm的測微表估讀誤差引起的標準不確定度取代了重復性測量誤差，其可行性、合理性令人疑惑。接著，在“A.3.5輸入量ai的不確定度u(ai)的計算”中有:
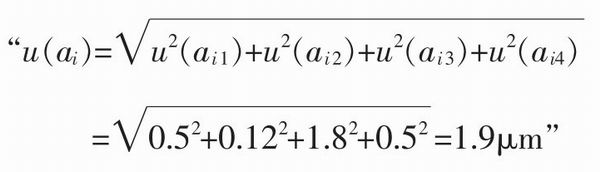
由此可見，相當于合成不確定度的u(ai)是由以上4個分量合成的，且第三分量――平板平面度引起的標準不確定度分量u(ai3)為主要因素，占總量的94.7%!其余的3個分量都微不足道。但是，經過以下分析和計算，情況卻發生了截然相反的轉變。
三、莫名其妙的表述問題
在“表A.1標準不確定度匯總表”中出現了4個完全一模一樣的“不確定度來源”:“測微表示值誤差、測微表的估讀誤差、平板平面度、圓柱直線度誤差”，且各自的“標準不確定度值u(ai)”均為完全相同的1.9μm。經過此絕無僅有的表達和計算，合成標準不確定度演化為: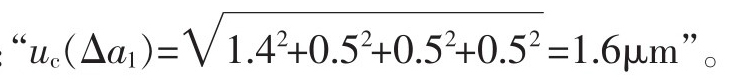
由該第二次的合成不確定度計算公式可見，第一分量u(a1)占總量的87.5%。由于“不確定度來源”中的各分量均為相同的4項誤差，故已無法確定為具體的某因素，但按序應認為是由示值最大允許誤差僅為±1μm的測微表引起的標準不確定度分量，莫名地轉變為主要因素；而原來極大的第三分量卻顯著變小，并與另外兩個分量無絲毫差別。
四、測量模型和靈敏系數的問題
之所以JJG194-2007得出以上錯誤的計算結果，完全是因為“A.4合成標準不確定度評定”以下的問題所致。
在“A.4.1靈敏系數”中有:“測量模型:
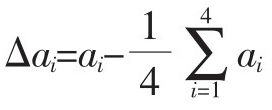
對某一工作面的垂直度有:
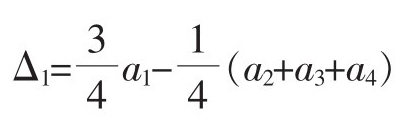
靈敏系數: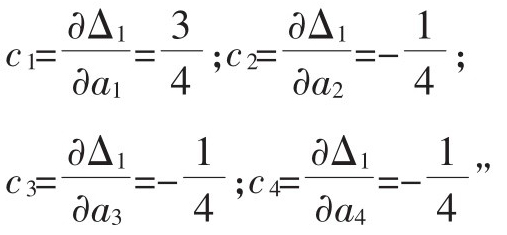
此所謂的“某一工作面的垂直度”，其實是對特定的第一只角(比如左上角)測量誤差的另類計算公式。明擺的簡單明了的數學模型(下面另有評價)不用，非得用此繁瑣的計算公式，典型的“避易就難”。由于此另類計算公式不具有代表性，并且還可衍生出另有的3個角(依次為左下、右下和右上角)的測量誤差計算公式，分別為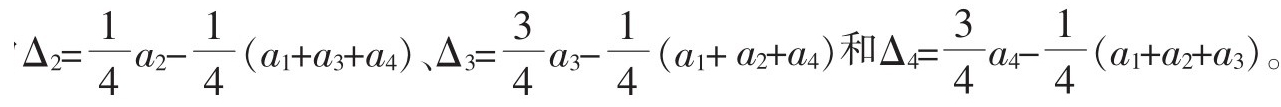
因此可得出各不相同的靈敏系數。正是由于該多此一舉的“節外生枝”問題，所以產生了如上一系列的錯誤，并導致以下的結論性問題。
這樣以下的數據處理就相當簡單了。因殘差計算式的靈敏系數的絕對值均等于1，故直接可以由A.3.5求得u(ai)=1.9μm(排除u(ai2)等的問題)，得出垂直度擴展不確定度為:U=3.8μm(k=2)。當然，這里存在一個同樣的問題:由平板的平面度誤差引起的標準不確定度分量u(ai3)究竟應該如何分析？是否確實有這么大？筆者認為:平板是測量方箱垂直度時的平面基準器具。作為標準，在分析由平面度對垂直度的影響而引起的不確定度時，是否可以考慮以相應平板的測量不確定度作為依據值得商榷。比如，以量塊為標準，在分析其測量不確定度時，一般都不直接以量塊相應規格、級別的“長度極限偏差”作為依據，而普遍都以量塊相應等別的“長度測量不確定度允許值的計算公式”作為依據。
五、JJG194-2007的結論性問題
JJG194-2007以邊長250mm的1級方箱(相應的垂直度允許誤差為10μm)為例，最終得出:“垂直度擴展不確定度為:U=3.2μm，滿足U≤1/3垂直度要求。證明本規程用圓周封閉法測量方箱垂直度誤差的檢定方法是科學、合理、可行的。”
該似是而非的結論是經不起推敲的。原因:測量不確定度評定中僅有的4個分量，無一是與被測量方箱的規格/邊長有關的變量，換言之:該4個分量都是不隨被測量方箱的邊長而以一定關系變化的固定常數。即JJG194-2007中列舉的6種方箱規格:邊長分別為100mm、160mm、200mm、250mm、315mm和400mm(對應的垂直度允許誤差分別為7μm、8μm、9μm、10μm、11μm和13μm)，它們的垂直度擴展不確定度均應為不變的U=3.2μm，這對于邊長≤200mm的方箱，并不滿足U≤1/3垂直度的要求。顯然，JJG194-2007疏忽了這一問題。
解決該問題的方法，筆者認為大致可以有以下3種方案:
(1)增加重復性測量誤差，刪去測微表估讀誤差。根據經驗，重復性測量誤差與被測量的規格大小成正比關系，卻與被測量的級別高低成反比關系，是為普遍規律。
(2)應該選用更高級別的00級平板，JJG194-2007適時的《平板檢定規程》為2005版，JJG194-2007中規定的400mm×600mm，在2005版《平板檢定規程》中規定00級平板的平面度最大允許誤差為3.5μm。于是u(ai3)=0.875μm，則
1.13μm， U=2.3μ
m，可保無虞。至此，不得不再提示一點:選用400mm×600mm平板作為方箱的平面基準器具，其平面的面積似乎局促了些。
(3)適當、合理地放大方箱工作面的垂直度誤差要求。
六、數據處理的準確度問題
JJG194-2007最終得出的結果U=3.2μm，兩位有效數據，其間數據處理過程中也只有1～2個有效數據，是不合理的，理應多保留1位，這是基本常識。
七、結束語
JJG194-2007中的附錄A“方箱垂直度測量結果不確定度評定”，存在的問題是顯而易見的。JJG194-2007“A.7結論”中的有關敘述，是經不起科學推敲的，其合理、可行性自然當受質疑。
