首頁>技術中心>技術資訊>三偶補償法在瞬態高溫氣流測量中的應用
三偶補償法在瞬態高溫氣流測量中的應用
發布時間:2017-09-01
引言
在新式武器裝備的設計階段,往往需要對一些關鍵部位的熱工參量進行準確測量,以驗證其設計參數。以某預研型號的發動機為例,其氣流理論溫度在1800 ~ 2000 K,但持續時間很短,同時氣流的靜壓非常低,只有幾千帕 ( 絕壓) 。在這樣的條件下,如果使用一般的屏蔽式熱電偶測量,由于無法達到熱平衡,響應慢,測量誤差甚至高達 1000 K[1]。因此,只能使用裸露式溫度傳感器來進行測量,但用裸絲結構進行直接測量也會有 100 ~ 400 K 的測量誤差[2]。文中介紹的三偶補償法就是針對這種高溫、高速、低壓及瞬態的測量環境設計的。
1 溫度傳感器測量原理
在高溫氣流的溫度測量中,產生的測量誤差主要有導熱誤差、速度誤差和輻射誤差[3]。下面就從這三個方面來分析溫度傳感器的測量原理和測溫偏差。
1. 1 單支裸絲的測量誤差
1) 導熱誤差
通常熱電偶導桿的直徑相對其長度尺寸很小( L/d > 20) ,對于這類細長構件,可以認為其溫度只在軸線方向上有變化,在橫截面上是均勻一致的,即可以視為一維問題。在一定的條件下,由于其長徑比很大,在熱接點附近幾乎不發生熱傳導現象,也就是說其導熱誤差可以忽略不計。
2) 輻射誤差
對于溫度傳感器輻射誤差的分析,通常將其看作置于密閉空腔中的小物體,不論壁面是何種材料,其中的輻射場都具有黑體輻射場的特性.
式中: Tg為氣體有效溫度; T 為溫度敏感元件的指示溫度; Tw為腔壁溫度; ε 為溫度敏感元件的表面發射率; σ 為斯蒂芬 - 玻爾茲曼常數; h 為對流換熱系數。
3) 速度誤差
溫度傳感器的速度誤差在氣流馬赫數超過 0. 2 時就比較明顯了
式中: ΔTv為溫度傳感器的速度誤差; T*為氣流總溫。
速度誤差通常根據恢復系數 r 來計算:
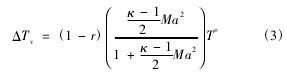
式中: r 為溫度傳感器的恢復系數; κ 為絕熱指數;Ma 為氣流馬赫數。
1. 2 三偶補償溫度傳感器
在一般的雙偶測量方法中,雙偶補償溫度傳感器在修正輻射誤差時,需要忽略壁溫進行計算。但在本文的條件下,壁溫在計算中是不能忽略的,而壁溫的準確值很難準確測得[4]。為了既考慮壁溫的影響,同時形成封閉物理方程組,人們就提出了用三支不同直徑的熱電偶同時測量高溫氣流的溫度,即所謂的三偶補償法。
三偶補償溫度傳感器由粗細不同的三對熱電偶組成,其接點結構應保持相同。測量時利用三對熱電偶的示值,通過修正獲得氣流的真實溫度。
設三對熱電偶的直徑分別為 d1,d2,d3,相應的示值和對流換熱系數分別為 Tj1,Tj2,Tj3和 h1,h2,h3。三對熱偶材料相同,表面發射率均為 ε,壁溫為Tw。三對熱電偶均垂直于氣流。采取較長的浸入長度( L/d > 20) ,使導熱誤差降低到可以忽略的程度。于是三對熱電偶可以分別寫出:

通過計算可以解出完全消除輻射誤差的有效溫度Tg。盡管從理論上分析三偶法是比較完整的,但其中有一些理想條件的假設,導致誤差較大,且由于實際問題的復雜性、小信號測量中的測量誤差使最終計算結果不很可靠。一是安裝角度的偏差會對式 ( 7) ~( 9) 有影響; 二是由于輻射誤差與實際溫度有著4 次方的強函數關系,其測量誤差的傳遞結果也是比較大的。所以實際使用中很少通過解方程組的方法來求得其有效溫度,而是通過數學方法對三對熱電偶的示溫度進行處理,從而推出在 d = 0 時的有效溫度,即視為消除輻射誤差的氣流有效溫度。
1. 3 零直徑外推法
零直徑外推法就是應用幾個直徑不同的熱電偶來測量氣流的溫度,根據這些溫度的讀數,用作圖法外推熱電偶直徑等于零時的溫度值,從而求得氣流的真實溫度。
試驗中的氣壓較低,能適用于雷諾數很小的Nusselt 準則方程為[5]:

從式 ( 10) ,( 11) 可以看出,當 d 趨近于零時,Nu 也趨近于零。因此,將實驗所得的線性 Tx- d 關系線性外推到 d = 0 時的 Tx即為所測氣流的有效溫度。實踐證明,此法相當準確。
2 現場試驗結果及數據處理
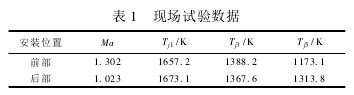
現場試驗是在瞬態、低壓、高溫、高速的條件下進行的,試驗器內靜壓為 2177. 26 Pa,理論溫度在1800 ~ 2000 K 左右,氣流馬赫數為跨音速。試驗中使用三偶補償式溫度傳感器對氣流溫度進行測量,偶絲分度號為 B 型,偶絲的直徑分別為 0. 1,0. 3,0. 5 mm。溫度傳感器分別安裝在試驗器前部和后部進行兩次試驗。兩次試驗數據見表 1,其中 Tj1,Tj3,Tj5分別為絲徑 0. 1,0. 3,0. 5 mm 熱電偶的指示溫度,Ma 為氣流馬赫數。
2. 1 前部數據處理
由于采取了大的長徑比 ( L/d > 20) ,所以溫度傳感器的導熱誤差可以忽略不計。
1) 輻射誤差
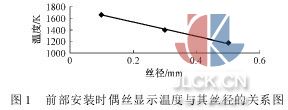
由于三偶補償法測量不能通過計算得出較準確的輻射誤差,所以需要運用零直徑外推的方法對測量結果進行修正[6]。三偶溫度傳感器分別選用了絲徑不同的三組熱電偶,由測量數據可以看出,其輻射誤差隨著絲徑變細而減小,當偶絲直徑趨近于零時,其輻射誤差也趨近于零。對試驗數據進行線性擬合,得出( 線性曲線見圖 1) :
d = 0,可得 Tg前= 1769. 2 K。即在溫度傳感器安裝在試驗器前部時,其測得消除輻射誤差后的氣流有效溫度為 1769. 2 K。
2) 速度誤差
由于實際測量出的馬赫數 Ma前= 1. 302,溫度傳感器處在超音速的氣流環境中,但偶絲的熱結點處感受到的為激波后的氣流速度,其波后馬赫數為

其中,r = 0. 7,κ = 1. 433,將其代入式 ( 14)中,可得總溫 T*前= 1834. 1 K,其速度誤差 ΔTv前=T*前- Tg前= 64. 9 K。
2. 2 后部數據處理
后部數據處理與前部數據處理方法完全相同,參照 2. 1。
1) 輻射誤差
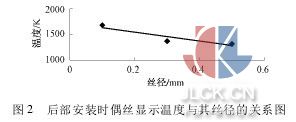
對試驗數據進行線性擬合,得出式 ( 15) 。線性曲線見圖 2。
令 d = 0,可得 Tg后= 1720. 9 K。即在溫度傳感器安裝在試驗器后部時,其測得消除輻射誤差后的氣流有效溫度為 1720. 9 K。
2) 速度誤差
實際測量得出馬赫數 Ma后= 1. 023, 參照式 13) 可計算出波后馬赫數 Ma'后= 0. 978。參照式( 14) 并將 r = 0. 7,κ = 1. 433 代入方程式中可得氣流總溫 T*后= 1814. 2 K,其速度誤差為 ΔTv后= T*后- Tg后= 93. 3 K。
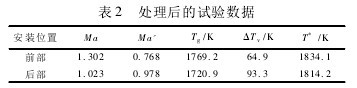
綜上所述,得出表 2 數據,可以看出測得的氣流總溫與理論值基本吻合。在兩次試驗工況比較接近的情況下,溫度傳感器分別安裝在試驗器的前部和后部,其測得的氣流總溫也比較接近,表明三偶補償式溫度傳感器比較適合用于測量該試驗器內的氣流溫度。
3 結論
三偶補償式溫度傳感器結構簡單,可以克服屏蔽式溫度傳感器和裸露式溫度傳感器的缺點。對于這種瞬態、低壓、高速、高溫條件下的溫度測量,三偶補償式溫度傳感器是適宜的。這種方法既可以修正裸露式溫度傳感器在高速高溫氣流中相對較大的速度誤差和輻射誤差,同時也彌補了屏蔽式熱電偶在瞬態高溫氣流中響應速度慢的缺點[7]。
摘自:中國計量測控網







