雙筒式減振器的熱力學模型
發布時間:2017-09-01
目前,車輛上廣泛應用的雙筒式液壓減振器工藝簡單、成本低廉,但散熱困難。因為它主要通過阻尼閥對油液節流產生阻尼力衰減車身振動,所消耗掉的振動能量將轉換成為熱能,使缸體溫度不斷升高。當缸體溫度達到并超過密封件所能承受的極限溫度后很容易導致油液的泄漏。雖然減振裝置的散熱能力對系統可靠性影響很大,但由于涉及不少跨學科專業知識,所以國內還沒有展開相關的研究工作,國外公開出版的文獻也甚少。基于這種情況,本文對雙筒式減振器的熱力學模型進行了系統研究。
1熱力學物理模型
建立的雙筒式液壓減振器熱力學物理模型如圖1所示。將兩只缸筒套裝在一起,在內筒中形成了減振器的工作室,內外筒之間為儲油腔,用來儲存和補償工作室中的油液;儲油腔中通常充有一定壓力的空氣,按照常規設計,可設其中油液占儲油腔容積的一半;活塞桿下端裝有活塞,在內筒中起支承和導向作用,并將工作室隔離為上下兩腔;活塞上安裝有壓縮和復原閥,通過對油液節流產生阻尼力衰減車身的振動;底閥將下腔與儲油腔隔離開,具有泄流及向工作室補充油液的作用,以防止減振器出現空程性畸變。
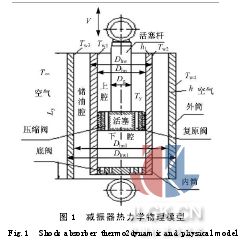
圖1中,Dhw為內筒外徑;Dhw1為外筒外徑;Dhn為內筒內徑;Dhn1為外筒內徑;Dg為活塞桿直徑;Ty為油液溫度;Tw1為內筒內壁溫度;Tw2為內筒外壁溫度;Tw3為外筒內壁溫度;Tw4為外筒外壁溫度;h為外筒壁厚;h1為內筒壁厚;T∞為外界環境溫度;V為活塞桿運動速度;Ly為缸筒長。
2熱力學數學模型
2.1生熱機理
如圖1所示,在工作過程中雙筒式減振器阻尼力所消耗的振動能量被用來增加油液分子的熱力學能,宏觀上表現為油液溫度的升高,其能量的傳遞關系為:在初始時刻,缸內溫度與環境溫度相同。壓縮行程時,下腔部分油液通過活塞上的壓縮閥進入上腔,以補充其增大的容積;另一部分油液則通過底閥進入儲油腔。在油液流過阻尼閥時,由于速度很快,流體與外界的熱量交換通常很少,但在阻尼閥附近會產生渦流、擾動(流體的內摩擦)等現象,所以節流是典型的存在內摩擦的絕熱流動過程。理論上講,流過阻尼閥的油液所產生的動能與增加的熱力學能之和同壓縮阻尼力做的功是守恒的,當下腔油液通過閥組分別進入上腔和儲油腔后,將與兩腔中的油液混合并發生熱力學能的變化;復原行程時,上腔油液通過活塞上的復原閥進入下腔,而儲油腔中的部分油液通過底閥也進入下腔以補充其增大的容積。同理,流過阻尼閥的油液所產生的動能與增加的熱力學能之和同復原阻尼力做的功是守恒的。當這兩部分油液進入下腔后,會導致油液熱力學能的再次變化,就這樣周而復始,最終油液溫度不斷升高。
2.2數學模型
減振器的熱量傳遞方式通常以熱傳導和熱對流為主。熱傳導又簡稱導熱,它是指熱量由物體的高溫部分向低溫部分的傳遞,或者由一個高溫物體向與其接觸的低溫物體的傳遞。當缸筒內外壁溫度不同時,就會在固體內部產生導熱現象。柱坐標系的導熱微分方程[1]為
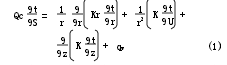
式中:ρ為缸體密度;c為缸體材料比熱容;λ為缸體材料導熱系數;qv為內熱源發熱率;t為攝氏溫度;τ為熱量傳遞的時間。
在減振器的工作溫度范圍內,缸體材料一旦確定,其導熱系數可設為常量,無內熱源時有qv=0;另外,缸體導熱的溫度場屬沿軸線對稱分布的一維導熱,所以式(1)可簡化為
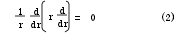
根據導熱微分方程和傅立葉定律聯合推導可分別得出內、外筒壁的導熱方程式
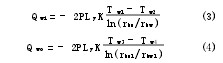
式中:Qwi、Qwo分別為內、外筒壁所傳遞的熱量。
在儲油腔中,設上半部分為帶有壓力的空氣,下半部分為油液。由于減振器工作時通常液面不會劇烈波動,所以儲油腔中的介質也主要以熱傳導的方式向外界散發熱量,根據式(2)及傅立葉定律可分別推導出空氣與油液的導熱方程式
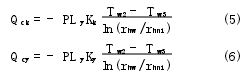
式中:λk為空氣的導熱系數;λy為油液的導熱系數;Qck為儲油腔中空氣所傳遞的熱量;Qcy為儲油腔中油液所傳遞的熱量。
聯立式(3)~式(6)并根據熱量傳遞關系整理得出熱傳導的綜合表達式為
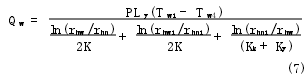
工程上遇到的大部分問題往往不是單純的熱對流方式,而是當流體流過不同溫度的固體表面時,依靠熱傳導和熱對流聯合作用的熱量傳遞過程,稱為對流換熱過程。減振器中工作室油液與內筒之間,外筒與環境之間的熱量傳遞都屬于對流換熱。
由傳熱學理論可知,空氣在外筒近壁處邊界層的發展不因空間限制而受到干擾,屬于大空間自然對流換熱。通過邱吉爾(S.W.Churchill)所提出的計算關聯式[2],可以推導出豎直狀態缸筒外表面換熱系數的表達式為
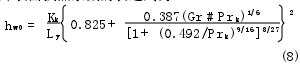
式中:格拉曉夫數為Gr =gβ(Tw4-T∞)L3yv2k;普朗特數為Prk=vkλkρkck,其中ck為空氣的比熱容;ρk為空氣密度;vk為空氣的運動黏度;β=1V
??Tp為容積膨脹系數,亦稱體膨脹系數。工作室油液與內筒之間屬于管內強迫對流換熱[3]。由凱斯推薦的努賽爾數特征關聯式[4-5]可推導出層流狀態下內筒內表面的強迫對流換熱系數為
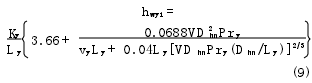
紊流狀態下內筒內表面的強迫對流換熱系數為

由式(7)和牛頓冷卻公式可推導油液散發到外界環境的熱量綜合表達式為
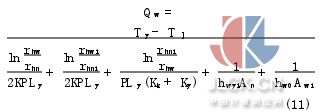
式中:Ahn為內筒內表面積;Aw1為外筒外表面積。以油液作為研究對象,根據能量守恒原理進行推導有
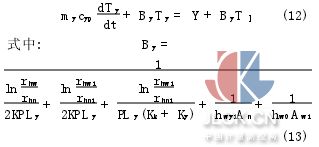
阻尼閥按小孔和縫隙節流計算,則有
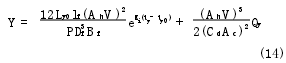
式中:my為油液質量;cyp為油液的定壓比熱容;ρy為油液密度;Ac為節流孔面積;流量系數Cd=0.62;δf為縫隙的寬度;Bf為縫隙的濕周;lf為縫隙的長度;μy0為油液的初始動力黏度;λi為油液的黏溫指數;Ah為活塞有效工作面積。聯立式(3)~式(13)即組成了雙筒式減振器的熱力學數學模型。
若將減振器外筒壁噴涂成黑色,則還需考慮熱輻射的換熱量。熱輻射換熱量的表達式[6]為
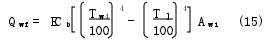
式中:黑體輻射系數Cb=5.67 W/(m2?K4);ε為熱輻射發射率。
推導外筒外壁的復合傳熱系數表達式為
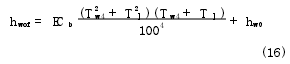
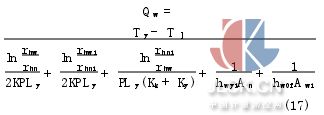
將式(16)與式(7)和牛頓冷卻公式聯合整理得出考慮熱輻射時油液散發到外界的綜合熱量表達式為
式(13)也改為
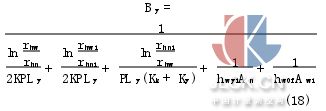
聯立上述所推導的各項表達式即組成了考慮熱輻射的雙筒式減振器熱力學數學模型。
2.3模型仿真分析
通過數學軟件Matlab編程對減振器的熱力學模型進行迭代運算。相關參數如下:δf=0.1×10-3m,Bf=0.25 m,Cd=0.62,lf=1×10-3m,λ=23 W/(m?K),T∞=300 K,ρy=890 kg/m3,λt=0.02,ρ0=1.293 kg/m3,T0=273 K,μy0=8.9×10-3kg/(m?s),節流小孔面積取為Ac=1×10-4m2。系統的初始溫度與外界環境溫度相等,激勵為振幅A=0.05 m的正弦曲線,頻率取為f=1 Hz。為便于分析,設減振器每工作一個循環,就與外界交換一次能量,循環次數X=5000,單次循環時間t=1/f。
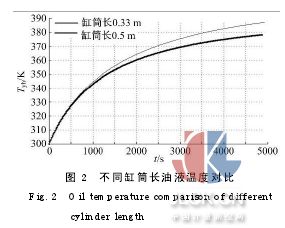
(1)設定減振器的基本結構尺寸為:Dhn=0.065 m,Dhw=0.07 m,Dhw1=0.09 m,Dhn1=0.085 m,Dg=0.026 m,Ly為0.33 m和0.5 m,仿真結果如圖2所示。
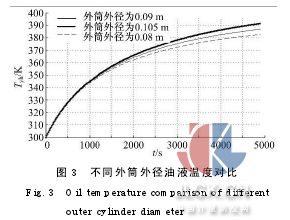
(2)設減振器的基本結構尺寸為:Dhw=0.07m,Dhn=0.065 m,Ly=0.33 m,Dg=0.026 m,Dhw1取為0.08、0.09、0.105 m,Dhn1取為0.075、0.085、0.1 m,仿真結果如圖3所示。
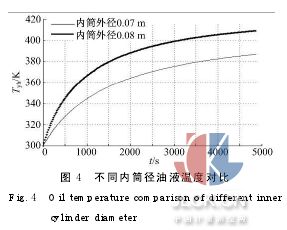
(3)設減振器的基本結構尺寸為:Dhw1=0.09m,Dhn1=0.085 m,Dg=0.026 m,Ly=0.33 m,Dhw取為0.07、0.08 m,Dhn取為0.065、0.075 m,仿真結果如圖4所示。
(4)設減振器的基本結構尺寸為:Dhw=0.07m,Dhn=0.065 m,Dhw1=0.09 m,Dhn1=0.085m,Ly=0.33 m,Dg為0.02 m、0.026 m,仿真結果如圖5所示。
由圖2可以看出,減振器其他參數確定后,筒長為0.33 m時,循環末端油液溫度為387 K;當筒長為0.5 m時,循環末端油液溫度為378 K。即隨著缸筒長度的增大,油液在相同時間內的溫升逐漸減小。
由圖3可以看出,在減振器缸筒壁厚及其余參數確定后,當外筒外徑為0.08 m,內徑為0.075m時,循環末端油液溫度為383 K;當外筒外徑為0.09 m,內徑為0.085 m時,循環末端油液溫度為387 K;當外筒外徑為0.105 m,內徑為0.1 m時,循環末端油液溫度為392 K。即隨著減振器外筒徑向尺寸的增大,油液在相同時間內的溫升逐漸增大。
由圖4可以看出,在減振器缸筒壁厚及其余參數確定后,當內筒外徑為0.07 m,內徑為0.065m時,循環末端油液溫度為387 K;當內筒外徑為0.08 m,內徑為0.075 m時,循環末端油液溫度為409 K。即隨著內筒徑向尺寸的增大,油液在相同時間內的溫升逐漸增大。
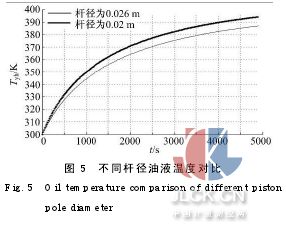
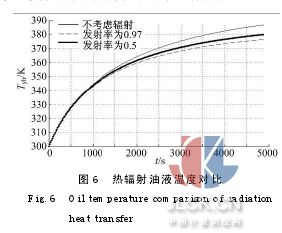
由圖5可以看出,在減振器其他參數確定后,當活塞桿直徑為0.02 m時,循環末端油液溫度為394 K;活塞桿直徑為0.026 m時,循環末端油液溫度為387 K。即隨著活塞桿徑向尺寸的增大,油液在相同時間內的溫升逐漸減小。圖6為熱輻射油液溫度的對比圖。由圖6可以看出,不考慮熱輻射時,循環末端減振器油液溫度為387 K;在把外筒壁面噴涂成深色后,發射率逐漸增大,這時就需要考慮熱輻射的換熱量。當發射率為0.5時,循環末端油液溫度為380 K;當發射率為0.97時,類似于黑體輻射,循環末端油液溫度為377 K。即隨著缸體發射率的增大,油液溫度在相同時間內的溫升逐漸減小。
通過上述分析可知,在阻尼閥結構尺寸不變的情況下,隨著缸筒軸向尺寸以及活塞桿徑向尺寸的增大,相同時間內減振器油液溫升逐漸減小;隨著內外缸筒徑向尺寸的增大,相同時間內減振器油液溫升逐漸增大;當減振器外表面噴涂深色或黑色漆后,隨著表面熱輻射發射率的增大,相同時間內減振器油液溫升逐漸減小。
另外,由以上各圖可以看出,隨著時間的增加,油液溫度逐漸趨于穩定,這是因為阻尼閥節流所產生的阻尼力與油液黏度有關。油液溫度上升,分子運動加劇,黏度迅速降低,阻尼力不斷減小,所消耗的振動能量以及轉換的熱量也減少,而隨著缸體溫度的升高,系統與外界環境溫差越來越大,散熱量不斷加大,所以系統最終將達到一個溫度的平衡點。
3結論
(1)阻尼閥結構參數不變時,增大缸筒軸向尺寸以及活塞桿的徑向尺寸,或者減小內外缸筒的徑向尺寸,都能夠使減振器油液溫升降低。
(2)為了增加系統散熱量,可在減振器外表面噴涂深色或黑色漆,提高熱輻射發射率,從而有效減緩油液的溫升速度。
(3)隨著時間的推移,系統將達到溫度平衡點,通過調整減振器的相關參數,將平衡點控制在密封件極限溫度范圍內,這樣可以避免泄漏。
摘自:中國計量測控網







