首頁>技術中心>技術資訊>基于多光譜法的目標真溫及光譜發射率自動識別算法研究
基于多光譜法的目標真溫及光譜發射率自動識別算法研究
發布時間:2017-09-01
多光譜測溫法是利用多個光譜下的物體輻射亮度測量信息,經過數據處理得到物體的真實溫度及光譜發射率.由普朗克定律可知,對于有n個通道的多波長溫度計來說,共有n個方程,卻包含(n+1)個未知量,即目標真溫T和n個光譜發射率ε(λi,T),因此必須假設光譜發射率與波長之間存在著某種函數關系,否則方程組無解.在多光譜輻射測溫領域常假設光譜發射率隨波長的變化而變化[1~3],其中一個常用的假設方程如下式所示
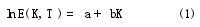
式中:λ為波長;T為物體的真實溫度.基于該方程,可通過最小二乘法計算出目標真溫及光譜發射率[4].當被測目標光譜發射率隨波長變化的真實情形與假設方程相符時,通過計算得到的真溫及發射率數據相當精確,但當二者不相符時,得到的計算結果偏差相當大[5].問題的關鍵在于我們對某種未知材料進行測量時,事先并不知道此種材料的光譜發射率與波長之間屬于哪種函數關系,因此采用任何形式的假設方程進行多光譜溫度計的數據處理都是盲目的、不科學的.鑒于上述原因,我們認為應該仔細研究各種被測材料的內在特性,努力找出它們之間的共性才是解決問題的關鍵.通過分析,我們確認材料的光譜發射率隨溫度的變化而變化是客觀存在的,又受處理非線性問題時常常要分段線性化的啟發,因此假設材料的光譜發射率在所選定的波長處與溫度有近似相同的線性關系,如下式
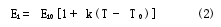
式中:εi0是波長為λi、溫度為T0時的光譜發射率;T0為某個初始溫度.
對于實際物體來說,上述假設在一定溫區、一定波長范圍內是普遍成立的.
1基本原理
此處提出的算法原理如下:①通過第1個溫度處各測量通道的輸出值以及第1個溫度的估計值,由計算獲知第1個溫度處的各光譜發射率的估計值.②使第1個溫度處通過計算獲得的各光譜發射率的估計值在某一范圍內變化.③通過假設方程式(2)可獲知第2個溫度處各光譜發射率的計算值.④對于第2個溫度處不同組的光譜發射率,可以計算出不同組的各波長下的真實溫度.當其中某一組各波長下的真實溫度的方差最小時,即為所求的第2個溫度處的真實溫度.因為只有當假設方程式(2)與被測目標的真實情形相接近或一致時,各波長下真實溫度的計算值才會趨近于同一數值.⑤進而可獲知第2個溫度處各光譜的發射率、第1個溫度處各光譜的發射率以及第1個溫度處的真實溫度.其算法詳細介紹如下.
如果多波長溫度計有n個通道,則第i個通道的輸出信號Vi可表示為
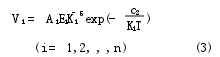
式中:Ai是只與波長有關而與溫度無關的檢定常數,它與該波長下探測器的光譜響應率、光學元件透過率、幾何尺寸及第一輻射常數有關.在某定點黑體參考溫度TR下,第i個通道的輸出信號ViR為
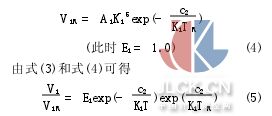
記Vi1為第1個溫度下、第i個通道的輸出信號,T0為第1個溫度的估計值,則第1個溫度下、第i個波長處發射率的估計值εi0為
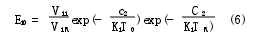
選擇ε>0,η>0,M>0,εi1∈(εi0-ε,εi0+ε),k∈(-η,η),T∈(T0-M,T0+M),則第2個溫度T處的發射率模型為
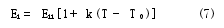
由于對不同的i可求出不同的T,故用Ti2表示第2個溫度下λi處的計算溫度值,則由式(5)可得
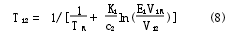
式中: Vi2為第2個溫度下第i個通道的輸出信號.由式(7)和式(8)可得
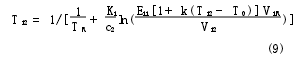
式(9)是關于Ti2的方程,可通過迭代法求解.此算法建立的準則是Til的方差極小化,即
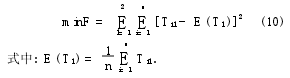
2實驗結果
作為被測目標的兩個不同溫度處多波長溫度計的輸出是按下述條件計算得到的:①兩個溫度點選為1 800 K和2 000 K;②定點黑體的參考溫度選為1 600 K;③八波長溫度計的有效波長為0?4、0?5、0?6、0?7、0?8、0?9、1?0、1.1μm;④1 800 K下各波長處的發射率模型如表1所示;⑤2 000 K下各波長處的發射率模型由εi(2 000)=εi(1 800)[1+k(2 000-1 800)]計算得到.
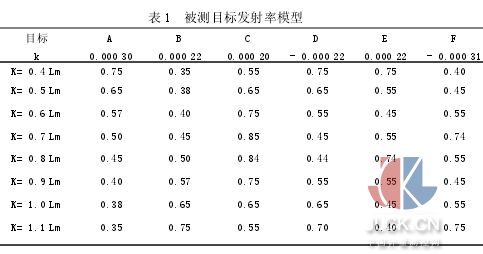
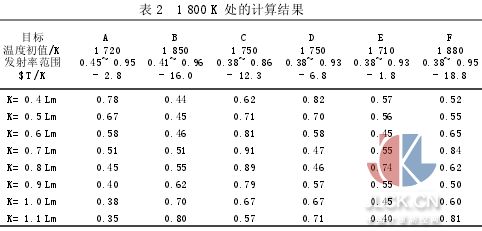
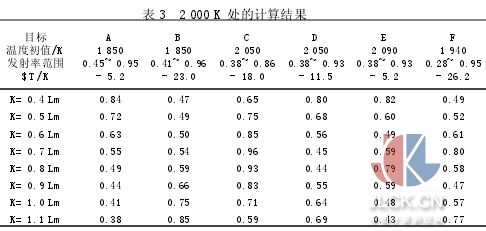
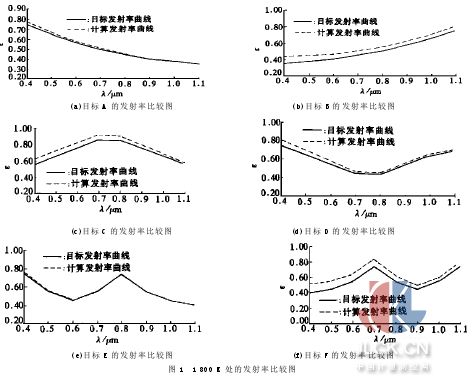
1 800 K、2 000 K處的溫度及光譜發射率的計算結果分別見表2、表3.表中ΔT=Tc-T ,其中Tc為計算溫度,T為目標真溫.1 800 K處的光譜發射率曲線與計算光譜發射率曲線見圖1.
3結論
本文提出的方法是通過處理兩個不同溫度處的測量數據來求取被測目標的真溫及光譜發射率,該方法對發射率與波長之間的函數關系不做任何限制,但要求發射率在所選定的波長處與溫度有近似相同的線性關系,這對于許多實際物體來說,在一定溫區、一定波長范圍內是不難滿足的.
由實驗結果可得出下述結論:①對于被測溫度點1 800 K和2 000 K,其溫度計算值對于A~F各種情形的相對誤差范圍分別為0?10%~1?04%和0?26%~1.31%;對于A~F各種被測目標,其發射率計算值隨波長變化的情況與真實情況相符,說明該方法可以很好地自動辨識如A~F情形的各種目標.②對于溫度初值來說,只要溫度估計初值與真實情況的誤差在±200 K以內,即可得到較好的計算溫度值和計算發射率值.③對于發射率搜索范圍來說,給定的搜索范圍與真實情況越接近,計算結果也越準確.④該方法不適合用于實時數據處理.
本文提出的方法用于實際測量時,其溫度初值可通過兩方面獲知:①有時可以通過純理論計算獲知,如固體火箭羽焰這種被測對象,通過純理論計算得到其真溫在2 150 K左右.②有時可以通過有經驗的技術人員目測得到.
綜上所述,本文方法的幾個約束條件在用于實際測量時并不難滿足,在不需要實時數據處理的場合,該方法是一種較實用的多波長溫度計的數據處理方法.
要說明的是,關于材料的光譜發射率在所選定的波長處與溫度有近似相同的線性關系的假設,還需在今后的研究工作中通過實驗加以證明.
摘自:中國計量測控網







