首頁>技術中心>技術資訊>雙半外圈調心球軸承預緊分析及在工程中的應用
雙半外圈調心球軸承預緊分析及在工程中的應用
發布時間:2017-09-01
1引言
雙列調心球軸承外圈滾道是球面的一部分,其曲率中心在軸承旋轉軸線上,具有自動調心的性能,一是用于補償由于軸的彎曲和軸承座孔變形產生的同軸誤差,二是在大型機構中,可以降低支撐結構的安裝調試精度指標。有不少學者對這類軸承的調心問題進行了研究[1-4],文獻[5]對這類軸承的徑向和軸向剛度進行了分析計算。成對雙聯向心推力球軸承在軸承生產中考慮到預緊變形量的大小,在相配對的兩個軸承的內圈或外圈的端面上,磨去一定的預緊變形量[6]。當將這種軸承安裝到軸承部件上時,用軸向預緊裝置壓緊相應端面,兩軸承即處于預緊狀態,磨削量可根據實際工作負載來確定。軸承預緊后,軸承的剛度和旋轉精度都能得到改善。很多學者對此進行了相關的研究[7-11]。
LAMOST天文望遠鏡像場旋轉軸兩個支撐點距離為1 938 mm,為了降低兩個支撐座孔同軸要求和加工調試成本,需要用可調心軸承來補償兩個座孔同軸偏差。另一方面,像場旋轉精度要求RMS值為1″,因此,支撐軸承需要進行消隙處理。這兩個要求實際上是雙列調心球軸承和雙聯向心推力球軸承的特點綜合。因此,本文采用了一種稱之為雙半外圈雙列調心球軸承,采用球面外圈實現調心功能,用兩個雙半外圈,在其中間加隔圈,通過控制隔圈的厚度來達到預緊的目的。采用這樣的軸承,實現了大角度調心和預緊提高剛性的雙重功能,保證了像場旋轉軸系的旋轉精度。跟星實測像場旋轉精度RMS值優于0.3″。這種軸承隔圈厚度的控制是實現高精度軸系的重要一環。首先根據對這類軸承的力學分析,得到相對于工作負荷的預緊力Fa0,然后根據三維接觸彈性理論,得出在Fa0的作用下,兩個半外圈的相對趨近量Δt,Δt就是中間隔圈的磨削量。經過磨削后的隔圈裝入軸承后,在壓緊裝置的作用下,實現了軸承的消隙,達到提高旋轉精度的目的。這類軸承,可以根據不同的工作負荷,磨削不同的隔圈,達到不同的預緊目的。
2預緊力和預緊量分析計算
2.1軸承結構
雙半外圈雙列調心球軸承結構如圖1所示。由雙半外圈、隔圈、鋼球、保持架和內圈組成。與傳統的雙列向心球面球軸承相比,其區別在于球面外圈由三部分組成:兩個內球面半外圈和中間隔圈。
(1)能夠實現較大的調心功能,調心角度達3°。
(2)能夠采用定位預緊,提高軸承的剛度。與現有調心球軸承1∶12錐面預緊相比,既降低了軸承和被支撐軸的加工成本,又不需要較大的軸向空間。
(3)軸承本身自成一預緊的封閉系統,這樣預緊力不會傳給被支撐軸。
(4)根據不同的工作要求,通過配磨中間隔圈的厚度,實現不同的預緊目的。
(5)這種軸承比較適合于低速、小加速度、無振動沖擊的場合,如天文望遠鏡軸系支撐等。
2.2預緊力的分析
在高精度的軸系中,軸承通常是在預緊狀態下工作的。通過預緊使軸承滾動體和內外套圈間產生一定的預變形,接觸面處于壓緊狀態,增加了軸承的剛度和提高了旋轉精度。另外,經過適當的預緊,能夠控制滾動體的自旋滑動,減少滾動體的公轉打滑等問題。
軸承預緊有徑向預緊和軸向預緊兩種,通常,多數采用軸向預緊。軸向預緊又分為定位預緊和定壓預緊兩種方式。預緊方式取決于軸系運轉的速度、加速度、工作環境(溫度、濕度)、潤滑情況等。本文討論的雙半外圈雙列調心球軸承應用于大型天文望遠鏡,運行速度和加速度都很小,也沒有沖擊和振動等問題,因此采用軸向定位預緊方式。在相同預緊變形量下,定位預緊比定壓預緊更能提高軸系的剛度。預緊方式如圖1所示。在兩個半外圈的端面上施加預緊力Fa0。軸承預緊力與變形的關系如圖2所示。圖中橫坐標為軸承外圈在預緊力作用下的軸向變形量δ,縱坐標為相應的軸向作用力F。
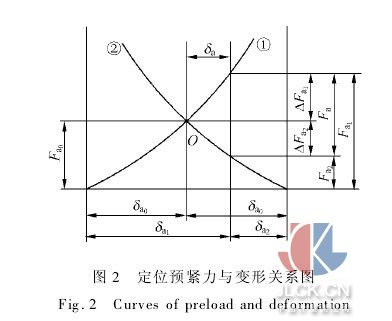
圖2中曲線①代表圖1中軸承右半外圈的變形情況,曲線②代表軸承左半外圈的變形情況。假設軸承定位預緊的預緊力為Fa0,在Fa0作用下,左、右半圈分別沿軸向向中間移動,曲線①和曲線②的交點O表示在Fa0作用下左半外圈和右半外圈的變形量均為δa0。當軸承外負荷在軸向的分力Fa作用在軸承上,并相應的產生δa的軸向變形。
這時,作用于軸承右半外圈的軸向載荷增加了ΔFa1,作用于軸承左半外圈上的軸向載荷減小了ΔFa2。
如增大Fa,使ΔFa2=Fa0,則軸沿Fa方向的移動量δa=δa0,此時,軸承的左半外圈完全不受負荷。
此時的Fa就是卸緊負荷Fau,根據球軸承負荷與變形之間的關系式[6]:
式中:δa為軸承內、外圈軸向相對移動量;Fa為作用于軸上的軸向載荷;Ka為軸承彈性變形系數;對軸承右半外圈而言。
為了保證軸承中兩列鋼球都能與兩個半外圈接觸,軸向定位預緊力為。
此處的Famax是軸承負載在軸向的分力,其中,包括徑向負載在軸向的分力。分析見后面的具體計算。
2.3預緊量的分析計算
軸承鋼球在預緊力的作用下,分別與外圈和內圈接觸,產生彈性變形。根據參考文獻[5]的分析計算,鋼球與內圈作用的彈性變形比與外圈作用的彈性變形小兩個數量級。因此,在本文的計算中,僅考慮鋼球與球面外圈之間的彈性變形。
根據三維接觸理論,兩球體在徑向力Fn作用下的徑向趨近量δ為[11]。
νball,νbearing:鋼球和軸承外圈的泊松比; Eball,Ebearing:鋼球和軸承外圈的彈性模量;R為綜合曲率半徑,1/R=1/Rball-1/Rbearing。
軸承在上面分析的Fa0作用下,可以認為整圈鋼球在軸向均與外圈接觸,且受力相等。
因此,在預緊力Fa0的作用下,根據Hertz接觸理論可得滾動體與球面外圈在軸向的趨近量為。
3應用實例
LAMOST像場旋轉軸前后兩個支撐軸承均采用雙半外圈雙列調心球軸承[12]。兩只軸承的間距為1 938 mm。內徑分別為:大軸承1 100mm,小軸承680 mm。兩只軸承如圖3所示。圖中軸承中間槽為配磨隔圈。被支撐軸及其負載總重量為5 852 kg。
從軸承結構圖(圖1)中的受力分析可以看出,軸承徑向負載Fr通過鋼球作用于雙半外圈,鋼球上的作用力對外圈產生軸向壓力。此軸向壓力的作用結果使得兩個剖分的球面外圈向外移。在計算軸承的預緊力時,也要考慮這一軸向分力。為此,需要先求出Fr在鋼球上的反作用力。
對于雙半外圈雙列調心球軸承而言,在徑向載荷Fr的作用下,軸承中兩列滾動體承受相同的載荷,每一列中最下面的滾動體載荷最大,滾動體載荷與Fr的關系為[6,13]:
式中:F0指右半圈最下面滾動體的載荷;F0′指左半圈最下面滾動體的載荷。注意:公式(15)中z指單列的鋼球數。
左、右兩列中其余相對應鋼球的載荷也相等,與最下面鋼球的載荷關系為:
式中:i為從最下面的一個鋼球沿圓周向上的鋼球數,i=1,2,…,int(z/4);ψ=360°/z,z為單列鋼球數;
由Fi產生的軸向分力為:
根據以上公式編寫Matlab程序,可以得到大、小軸承預緊力的數據表(表1)。
求得預緊力后,可根據公式(14)計算大、小軸承的預緊量,即隔圈的磨削量Δt。計算結果列于表2。
磨削后的隔圈裝上軸承后,用軸向壓緊圈將左半外圈和右半外圈壓貼在一起,可在軸承座上開觀測孔,用塞規進行實測。同時,用力矩扳手實測壓緊螺釘上的壓緊力。兩者結合起來保證預緊效果達到最佳。
隔圈磨削量Δt的加工精度會引起預緊力的偏差。大軸承隔圈外徑??1 299 mm,原始厚度40mm,小軸承的隔圈外徑899 mm,原始厚度30mm。磨削加工Δt后實測厚度偏差量分別為+13μm和+9μm。分別將Δt偏差量代入公式(14)進行反計算,可得由此引起的預緊力的變化量,大軸承預緊力變化量為162.70 N,占理論預緊力的2. 67%。小軸承預緊力的變化量為110.72 N,占理論預緊力的2.43%。由于熱變形和潤滑等原因,隔圈的磨削量取正偏差。
4總結
本文對LAMOST天文望遠鏡像場旋轉軸支撐軸承―――雙半外圈雙列調心球軸承的預緊力和預緊量的計算方法進行了探討,并給出了具體的計算實例。實際使用情況表明,這種計算方法是可行的。現場安裝預緊調整后實測表明,在任一50°范圍內軸系的徑向跳動(像場旋轉軸工作范圍)<0.02 mm,軸向端面跳動<0.03 mm。采用這種軸承,滿足了LAMOST項目對像場旋轉軸系剛度和旋轉精度的要求。跟星實測像場旋轉軸旋轉精度RMS值優于0.3″。
本文介紹的雙半外圈雙列調心球軸承的預緊是先通過理論計算出預緊量,而后精確配磨隔圈厚度來實現的。隔圈配磨量的加工精度會引起預緊力的偏差。因此,需要對配磨量加工精度提出相應的精度指標,以預緊力偏差低于總預緊力的5%為準。另外,此類軸承對于在其他地方的應用,如文中所提的0.35倍最大負載的預緊力,應根據具體的使用情況做針對性的適當調整,如軸承旋轉速度、加速度、工作溫度、負載波動、潤滑等。預緊力過大,雖然可以獲得較高的軸承剛度和抗載能力,但卻使軸承的摩擦力矩增大,而且容易出現“死點”,在高速下,軸承溫升較大,影響軸承的壽命。如果預緊力過小,軸承剛度減小,在存在較大的加速度和負載波動的情況下,容易發生卸載,出現間隙,影響傳動精度。因此,正確選擇預緊力的大小要綜合各方面的因素。
摘自:中國計量測控網







