首頁>技術(shù)中心>技術(shù)資訊>基于衍射理論的分塊鏡共相位誤差的高精度測量
基于衍射理論的分塊鏡共相位誤差的高精度測量
發(fā)布時間:2017-09-01
引言
大型望遠(yuǎn)鏡是物理學(xué)家及天文學(xué)家研究宇宙起源最重要的工具,望遠(yuǎn)鏡的集光能力及角分辨率隨著口徑的增大而增強(qiáng),集光能力越強(qiáng),就能看到越暗越遠(yuǎn)的天體,即能夠看到更早期的宇宙,天體物理的發(fā)展需要更大口徑的望遠(yuǎn)鏡。從16 世紀(jì)伽利略發(fā)明望遠(yuǎn)鏡到當(dāng)今美國加州理工大學(xué)建造的10 m 口徑的凱克望遠(yuǎn)鏡,主鏡口徑在不斷增大。但是,隨著望遠(yuǎn)鏡口徑的增大,一系列的技術(shù)問題接踵而來。首先,望遠(yuǎn)鏡的自重引起的鏡頭變形影響相當(dāng)大,鏡面畸變嚴(yán)重影響成像質(zhì)量[1]。其次,從制造成本來看,傳統(tǒng)方法制造望遠(yuǎn)鏡的費(fèi)用幾乎與口徑的平方甚至立方成正比[2],因此,從20 世紀(jì)80 年代開始,采用可收展式的分塊鏡的思想逐步發(fā)展起來[3],如圖1 所示。
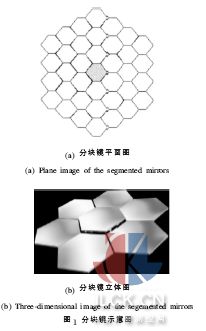
拼接式分塊鏡光學(xué)系統(tǒng)能滿足下一代太空望遠(yuǎn)鏡更大、更輕和可折疊的要求[4]。拼接鏡面即將一系列子鏡拼接在一起達(dá)到單一鏡面的光學(xué)性能。如果不采用分塊鏡共相位成像技術(shù),整個光學(xué)系統(tǒng)的分辨力將受限于單個分塊鏡的分辨力,分塊鏡共相位誤差的存在會嚴(yán)重影響成像質(zhì)量。分塊鏡光學(xué)共相位誤差與系統(tǒng)成像質(zhì)量之間存在如下關(guān)系[5]: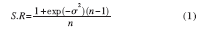
式中: S.R 為斯特列爾比, 是光學(xué)系統(tǒng)像質(zhì)評價的一種指標(biāo), 理想值為1;σ =2kδ = 4πλ δ ,λ 為波長,δ 為各分塊鏡鏡面之間高度差的均方根值;n 是分塊主鏡的數(shù)量。要保證系統(tǒng)具有優(yōu)良的像質(zhì),各分塊鏡之間高度差的均方根值要達(dá)到δ≤λ/20。沿光軸方向,分塊鏡之間的高度差即為共相位誤差,如圖1 (b)所示。分塊鏡在展開后首先進(jìn)行機(jī)械調(diào)整,將誤差范圍盡量減少,然后進(jìn)入合像環(huán)節(jié), 將傾斜等量檢測并校正到很小的范圍內(nèi),滿足共相位誤差的檢測要求。對于尺度為米級的大型分塊鏡而言, 要把各分塊鏡之間的共相位誤差檢測到λ/20 的精度水平, 是一個極具挑戰(zhàn)性的難題。因此, 分塊鏡共相位誤差高精度的檢測和校正是實(shí)現(xiàn)超大口徑、甚高分辨率成像的前提和技術(shù)關(guān)鍵。
分塊鏡共相位誤差的檢測通常采用分步測量的方法,用寬光譜光源進(jìn)行粗測,將共相位誤差的測量范圍減少到一個波長范圍內(nèi)。切換單色光光源,利用單色光實(shí)現(xiàn)納米級的高精度測量。美國在這方面的研究處于領(lǐng)先地位,Keck 地基天文望遠(yuǎn)鏡用PSF 法[6]實(shí)現(xiàn)共相位誤差的測量,該方法系統(tǒng)結(jié)構(gòu)簡單,但是計(jì)算量較大,測量周期長。美國加州大學(xué)的Gary Chanan等人發(fā)展了一種新的基于相位反演原理的分塊鏡共相位誤差檢測方法, 即相位反演法(PDS)[7]。目前,NASA 正在著手第二代太空望遠(yuǎn)鏡(NGST)的研制,提出了色散條紋法(DFS)[8]。這兩種方法的測量精度較高,但是系統(tǒng)較前者更為復(fù)雜,不利于空間環(huán)境下的高精度測量。我國在這方面的研究起步較晚,中國科學(xué)院光電技術(shù)研究所采用基于邁克爾遜干涉系統(tǒng)的拼接主鏡的共相位誤差檢測技術(shù)[9-11],該方法系統(tǒng)復(fù)雜,對噪聲較為敏感,很難適應(yīng)空間環(huán)境下的高精度測量。
文中研究相鄰分塊鏡之間的共相位誤差檢測,衍射光斑的峰值位置偏離中心位置的距離隨共相位誤差的變化規(guī)律,利用該理論實(shí)現(xiàn)一個周期范圍內(nèi)共相位誤差的高精度測量,并進(jìn)行了實(shí)驗(yàn)驗(yàn)證。該方法系統(tǒng)結(jié)構(gòu)簡單,所需像斑的采樣點(diǎn)少,有利于空間環(huán)境下的共相位誤差檢測。
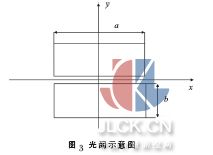
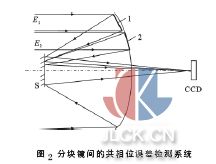
1 檢測原理
1.1 共相位誤差測量原理
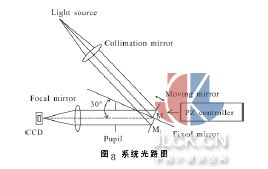
相鄰分塊鏡之間共相位誤差檢測系統(tǒng)如圖2 所示,E1和E2為入射平行光,1 和2 為反射鏡,1 和2 的連接處設(shè)置了方形光闌, 橫跨相鄰兩個分塊鏡,S 為次級反射鏡。入射光經(jīng)過光闌及反射鏡在焦面發(fā)生衍射-干涉,采用CCD 可以接收到衍射-干涉圖。圖3為方形光闌示意圖。其中a,b 分別為光闌的長和寬。當(dāng)分塊鏡1 和2 之間存在共相位誤差,E1和E2經(jīng)過反射鏡后存在光程差, 衍射光斑也會隨共相位誤差的變化而變化。入瞳函數(shù)為:
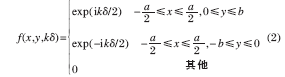
根據(jù)波動光學(xué)及傅里葉光學(xué)理論, 焦面處衍射-干涉圖的一維光強(qiáng)分布為: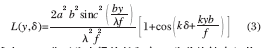
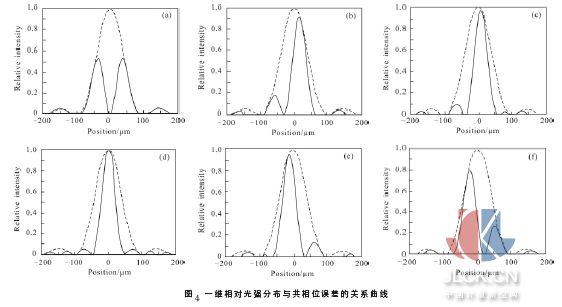
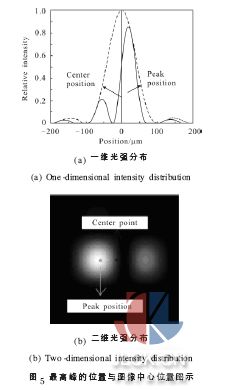
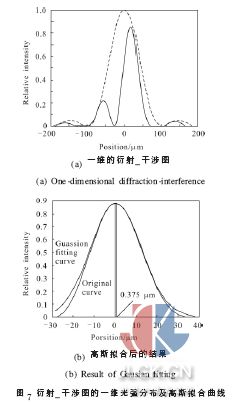
式中:a, b 分別為光闌的長和寬;δ 為分塊鏡之間的共相位誤差;k=2π/λ 。衍射-干涉圖隨共相位誤差的變化而變化,如圖4 所示,圖中,(a)~(f)是共相位誤差分別為-0.5λ ,-0.25λ ,-0.1λ ,0,0.15λ ,0.3λ 所對應(yīng)的一維衍射-干涉圖, 虛線為包絡(luò)曲線, 橫軸為位置坐標(biāo),縱軸為相對光強(qiáng)。衍射-干涉圖隨共相位誤差的改變而明顯不同。以圖像中心為參考點(diǎn),最高峰的峰值位置隨共相位誤差的變化而移動。圖5 為最高峰的峰值位置與圖像中心位置。共相位誤差為零時,最高峰位于圖像中心,隨共相位誤差的增大,最高峰上移(對應(yīng)y 平面為左移)。共相位誤差為負(fù)時,最高峰位于圖像中心下側(cè)(對應(yīng)y 平面為右移)。
1.2 最高峰位置與共相位誤差的關(guān)系
由公式(3)可知:衍射-干涉圖的光強(qiáng)分布是sinc函數(shù)和余弦函數(shù)的乘積,最高峰的峰值位置是該函數(shù)L(y,δ )的拐點(diǎn)位置。對函數(shù)L(y,δ )求導(dǎo)數(shù),導(dǎo)數(shù)為零的點(diǎn)即為拐點(diǎn),但是,該函數(shù)的導(dǎo)數(shù)沒有準(zhǔn)確的解析表達(dá)式,需要對該表達(dá)式進(jìn)行分析,得到零點(diǎn)位置。對公式(3)中的sinc 函數(shù)的平方在y=0 附近進(jìn)行泰勒展開:
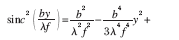

令L(y,δ )的一階導(dǎo)數(shù)為零,計(jì)算拐點(diǎn)位置。由于共相位誤差是10-7 量級,δ 的高次冪可以忽略, 經(jīng)過理論推導(dǎo)得到最高峰的位置與共相位誤差δ 的關(guān)系為: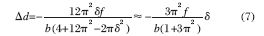
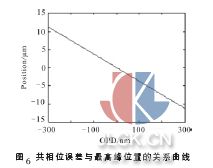
共相位誤差與最高峰位置之間近似為線性關(guān)系,仿真曲線如圖6 所示。橫軸為光程差,縱軸為最高峰相對于圖像中心的位置。共相位誤差為負(fù),最高峰處于圖像中心的左側(cè),隨著共相位誤差逐漸變小,最高峰位置逐漸右移。共相位誤差為零時,最高峰相對于圖像中心的距離為零。
1.3 峰值位置的確定
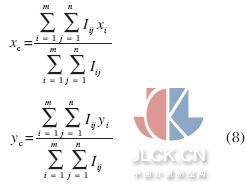
最高峰峰值位置的確定直接影響測量精度。根據(jù)共相位誤差與峰值位置的關(guān)系,可以確定采用可見光光源,如要滿足λ /20 的測量精度,最高峰的定位誤差需要控制在800 nm 的范圍內(nèi), 采用基于高斯擬合的峰值定位方法來確定最高峰的峰值位置。在光闌為 1 cm、焦距為0.5 m 的情況下,亮斑大約為60 μm。根據(jù)公式(8)計(jì)算圖像的質(zhì)心:
在質(zhì)心附近判斷最高峰的位置,然后設(shè)置閾值,提取最高峰。
在峰值兩側(cè)取點(diǎn)作高斯擬合。假設(shè)高斯擬合曲線表達(dá)式為:

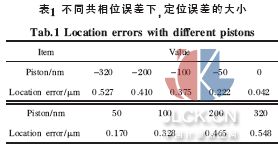
式中:m 為未知數(shù)個數(shù);n 為采樣點(diǎn)個數(shù)。在像元尺寸為5 μm、采樣點(diǎn)為10 個左右的情況下,該峰值定位方法的定位誤差小于600 nm,如表1所示,能夠滿足所要求的定位精度。圖7(a)為一維光強(qiáng)分布圖, (b)為在峰值左右取10 個點(diǎn)擬合得到的高斯曲線, 其峰值位置與原曲線的峰值位置誤差為0.180 μm。分析光闌的衍射-干涉圖的光強(qiáng)分布可以得出:在共相位誤差為零時,像斑中心為一個大的主峰,兩側(cè)有小的側(cè)峰,并且圖像中心對稱。隨共相位誤差的增大,像斑主峰逐漸變小,側(cè)峰逐漸變大,主峰的對稱性逐漸變差,當(dāng)這兩個峰一樣大即共相位誤差達(dá)到半波長時, 主峰的對稱性最差,但是定位誤差仍然在允許范圍內(nèi)。
2 實(shí)驗(yàn)
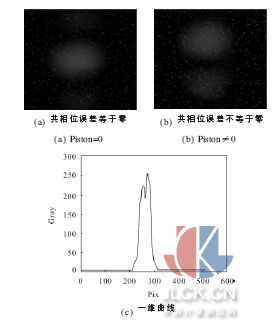
實(shí)驗(yàn)采用單色性強(qiáng)的He-Ne 激光器作為光源,光源發(fā)出的光經(jīng)過準(zhǔn)直透鏡,得到平行光,再經(jīng)過分塊鏡M1和M2,以及1 cm 的方形光闌,發(fā)生衍射-干涉,通過會聚透鏡得到衍射光斑, 采用CCD 接收衍射光斑圖像。M1和M2是從同一塊平面度很好的鏡子上切割下來的, 其中,M1為動鏡,M2為定鏡, 通過壓電陶瓷控制器來控制動鏡。會聚透鏡焦距為0.8 m。CCD像元尺寸為4.65 μm×4.65 μm,系統(tǒng)光路圖如圖8所示。用壓電陶瓷控制M1, 將M1和M2之間共相位誤差調(diào)為零,得到圖9(a),計(jì)算圖像的中心位置,零共相位誤差時,衍射光斑具有中心對稱性,光斑的質(zhì)心位置與中心位置重合,圖像的質(zhì)心即為中心位置,以此作為參考點(diǎn)。圖像是關(guān)于縱軸對稱的,圖像中心橫坐標(biāo)與質(zhì)心橫坐標(biāo)相同,不隨共相位誤差的變化而變化。
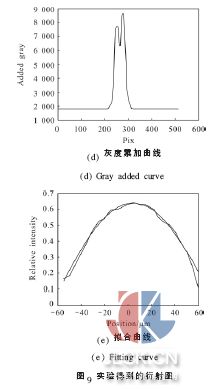
壓電陶瓷制動器控制動鏡,改變共相位誤差的大小,得到的衍射光斑如圖9(b) 所示, 其y 平面的灰度曲線如圖9(c)所示,縱軸為灰度值,橫軸為位置坐標(biāo)。由于衍射圖像質(zhì)心所在的縱軸對稱,圖像灰度進(jìn)行橫向疊加后,中心位置坐標(biāo)不變,而且灰度累加可以減少隨機(jī)噪聲的影響,減少定位誤差。所得到的縱向灰度曲線如圖9(d)所示,縱軸為灰度累加, 橫軸為位置坐標(biāo),利用上述的高斯擬合曲線確定衍射光斑最高峰相對于圖像中心的距離為14.393 μm, 如圖9 (e)所示。經(jīng)過計(jì)算共相位誤差為93 nm。壓電陶瓷的位移量為65 nm, 即共相位誤差值為65 nm, 測量誤差為28 nm。由于實(shí)際實(shí)驗(yàn)條件的限制,受噪聲及壓電陶瓷精度影響,誤差較大,但仍能滿足λ /20 的測量精度,該方法能夠有效檢測分塊鏡共相位誤差。
3 結(jié)論
通過以上分析可以得出如下結(jié)論:
(1) 一個波長周期范圍內(nèi), 衍射光斑最高峰的峰值位置偏離圖像中心的距離與共相位誤差之間呈線性關(guān)系。采用可見光光源,要達(dá)到λ/20 的精度,峰值定位精度要優(yōu)于800 nm。
(2) 基于高斯擬合的峰值定位方法的定位誤差小于600 nm,滿足定位要求,計(jì)算簡單, 適合該測量方法。且CCD 像元尺寸越小,定位精度越高。
(3) 利用衍射光斑的峰值位置判斷共相位誤差的方法是一種有效的測量方法,由于實(shí)驗(yàn)條件限制,振動及噪聲對衍射光斑有一定影響,使得誤差稍大,但實(shí)驗(yàn)結(jié)果表明:該方法的測量精度能達(dá)到λ /20。
摘自:中國計(jì)量測控網(wǎng)







