支撐面積對薄鏡面形影響的研究
發布時間:2017-09-01
引言
隨著空間光學系統和高功率激光系統向大口徑方向發展[1],系統主要光學元件的口徑不斷增大, 這極大地影響了整個光學系統的質量和體積,以及工程的成本。因此,通過減小元件厚度,使用薄型和超薄型光學元件來改善系統結構成為目前光學系統設計的主要方式[2]。但隨著光學元件厚度的降低,直徑厚度比的增大, 元件面形在使用過程中非常容易受到外界因素的影響(如重力作用、機械振動),導致光束質量的惡化,其中,鏡面的自身質量和支撐結構產生的鏡面變形尤為突出。考慮到鏡面支撐結構中軸向支撐比徑向支撐對鏡面變形的作用更大,因此,必須設計一套合理的支撐結構來盡可能地降低鏡面自重產生的變形,從而獲得較好的表面面形。另外,由于天文望遠鏡主鏡與高功率激光系統中的大口徑反射鏡在應用上的不同,它們對不同空間頻率范圍的面形畸變控制要求不一樣[3],因此,在設計支撐結構時,還必須考慮鏡面變形的空間頻率特性。基于此,利用有限元法對薄型鏡面變形情況進行分析,然后通過設計不同的支撐單元面積,分析元件面形變化, 最后分別從空間域與頻率域上分析了支撐單元大小對鏡面形狀的影響。
1 基本理論
由于可以將各種晶體或玻璃材料生產的光學元件看作彈性體,這樣在分析其變形過程時,可以利用彈性力學中的薄板彎曲小撓度方程犖2犖2 w=q/D 進行求解[4]。而該方程只有在環帶支撐情況下才具有解析解,對目前廣泛使用的多點支撐方案得不到解析結果,所以文中選擇有限元法來求解。
有限元法的基本思想是將連續體劃分為有限個在節點處連接的小單元,然后利用在各單元內假設的近似函數來分片逼近全求解域上的未知場函數。文中將二維圓板離散成若干個矩形單元,每一單元的模型如圖1 所示。圖中矩形單元兩邊長分別為2a和2b,有4 個節點(i、j、m、p),每個節點有3 個自由度( 沿z 軸方向的撓度w、繞x 軸的轉角θ x 、繞y 軸的轉角θy )。由于只受到沿z 軸方向重力的作用,利用最小位能原理建立有限元方程Ke ae =Pe [5],將矩形板單元中節點的位移表示成單位剛度矩陣與等效節點載荷的乘積。
E 為彈性模量;t 為矩形單元厚度;μ 為泊松比;ρ 為單元單位厚度的質量,即載荷。因此,將公式(2)帶入公式(1),再加上固支邊界條件,就可得到矩形單元節點的位移,然后推廣到整個模型,得到模型的撓度w,就可以計算模型各點的應力、P螄V 和RMS 值等,為研究面形的變化做準備。
2 有限元模型計算結果及分析
以K9 玻璃為鏡面材料,具體參數:彈性模量E=81.32 GPa,泊松比μ=0.209,密度ρ=2.53 g/cm3。光學元件口徑Φ200 mm,厚度h=10 mm。將其進行有限單元劃分后。
2.1 支撐單元面積對元件面形影響的空域分析
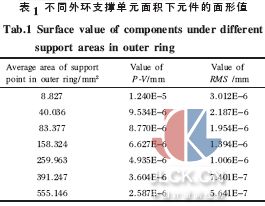
在光學元件上施加9 個支撐單元, 如圖3 所示。內環3 個支撐單元,距圓心25 mm,外環6 個支撐單元,距圓心70 mm,沿圓周均勻分布。在具體計算時對9 個支撐單元均施加全約束,首先固定內環3 個支撐單元的面積均為28.756 mm2,改變外環支撐單元的面積, 分析外環支撐單元大小對元件面形的具體影響;然后在固定外環6 個支撐單元的面積均為555.146 mm2,改變內環支撐單元的面積,分析內環支撐單元大小對元件面形的具體影響。圖4 為外環支撐單元面積變化得到的圖形。(a)、(b)、(c)的外環支撐單元平均面積分別為8.827 mm2、158.324 mm2、555.146 mm2。在有限元分析過程中,面積的計算由所劃分的有限單元大小決定, 考慮支撐單元面積的相對誤差在5%的合理范圍內,得到如下數據,如表1 和表2 所示。可以看出:相對于外環支撐單元面積,內環支撐單元面積的變化對面形的P螄V、RMS 值的影響不大, 內環支撐單元面積從0.8940 mm2 增大到28.756 mm2, 其P螄V 和RMS值分別變化了0.5%和9%。因此,文中主要研究外環支撐單元面積的變化對面形影響。
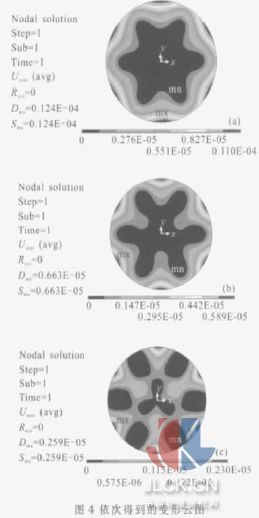
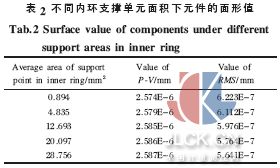
為了進一步分析外環支撐單元面積變化對面形的影響,通過圖5 和圖6 可以進行直觀的研究。
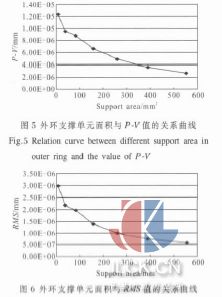
由圖5 和圖6 可以看出:隨著外環支撐單元面積的增大,鏡面的變形在減小,其P螄V、RMS 值逐漸減小,當外環支撐單元面積由8.827 6 mm2 增大到555.146 mm2后,其P螄V、RMS 值下降了大約80%。計算結果說明:外環支撐單元面積大小對空間域下的鏡面變形有明顯作用,通過增大外環支撐單元面積可以獲得較好的面形,這對于以后的工程設計有重要的參考意義。
2.2 支撐單元面積對元件面形影響的頻域分析
在高功率激光系統應用中,非常關注光學元件面形畸變在頻率域中的分布[3],利用一維PSD 曲線來具體分析支撐單元面積變化對元件面形畸變在頻率域中的影響。由圖4 可知:元件面形畸變具有對稱性,一維PSD 曲線可以較好地反映整個面變形情況的頻域信息。在計算中使用一維模型,如圖7 所示。
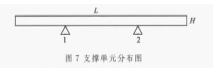
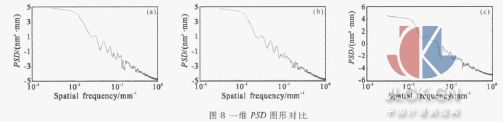
在模型中L=200 mm,H=10 mm,W=10 mm, 共401 個節點。設定在兩端簡支, 在1 和2 處的支撐單元施加固定約束,當支撐單元大小變化后,計算得到的PSD 曲線如圖8 所示,(a)、(b)、(c)在1 和2 處的支撐單元大小分別為5、7、13 mm。
從圖8(a) 可以看出: 此時由PSD 曲線反映出元件主要面形誤差分布在空間頻率大約為0.17 mm-1處。當支撐單元逐漸增大到7 mm 時,面形誤差的頻率分布沒有明顯變化,但是圖8(b)中顯示的突變值幅值在減小,也就是該頻段誤差值降低。繼續增大對稱支撐單元的長度,從圖8(c)可以看出:主要誤差頻率由0.17 mm-1 移向了0.2 mm-1,元件面形誤差已經進入了中頻段[7]。計算結果說明支撐單元的大小對波前誤差的空間頻率分布有明顯的影響,當支撐單元面積略微增大時,相當于減小了調制深度[8], 其突變值的幅度將減小;當支撐單元面積增大較多時,又相當于增加了調制頻率[8],其突變值的位置將向較高頻段移動。
3 結論
分析了薄型鏡面在多點支撐下,設計不同支撐單元面積而產生的鏡面變形情況, 通過計算P螄V、RMS值得知:從空域分析來看,支撐單元面積與光學元件面型之間的關系是增大外環支撐單元的面積可以明顯減小P螄V、RMS 值而獲得較好的面形; 從頻域分析的結果來看,支撐單元面積增大將使元件面形誤差向較高的空間頻段移動,甚至可以達到中頻段。對于空間成像系統而言,影響成像質量的主要是元件面形畸變的低頻段部分,而對于高功率激光系統而言,中頻段畸變信息將導致明顯的非線性破壞,因此,針對不同的應用應該合理考慮支撐單元大小的影響。經過初步分析可知,采用多點支撐方案進行大口徑光學元件的支撐時,如果在大口徑望遠系統中,可以盡量增大支撐單元的面積;而在高功率激光系統中,則不能使用過大的支撐面積,以免增加中頻段誤差。
摘自:中國計量測控網







