首頁>技術中心>技術資訊>液力變矩器三元流場計算的一種近似方法
液力變矩器三元流場計算的一種近似方法
發(fā)布時間:2017-09-01
1引言
液力變矩器的內(nèi)部流動是極為復雜的三維流動。為了能夠?qū)ζ溥M行求解,采作兩類相對流面的概念,并依此有了求解三元流動的普遍理論和方法。兩類相對流面的基本思想是把葉輪內(nèi)的三維流動問題,分解為兩個分別沿著S1流面和S2流面的相關二維問題,兩個流面相互迭代進行求解,直至滿足精度要求。然而,在兩類流面相互迭代求解的過程中,迭代求解的過程花費時間較長,還有可能出現(xiàn)求解不收斂的情況。于是本文提出了一種在兩類相對流面基礎上的液力變矩器三元流場計算的近似方法。該方法直觀性強,無繁雜的迭代運算,計算程序容易編制,使用計算機內(nèi)存少,計算時間短,且能滿足一定的精度要求,適合于工程應用。
2基本假設
為了進行液力變矩器三元流場的近似計算,作出如下基本假設:
(1)液力變矩器葉輪內(nèi)的流動是定常流動并且無空穴現(xiàn)象,工作介質(zhì)是理想流體;
(2)液流沿著S1流面的運動是有勢的;
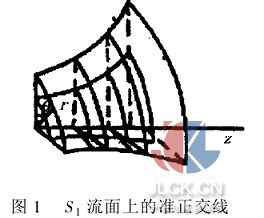
(3)流道中S1流面上的準正交線是S1流面上r和z均為常數(shù)的圓周線,即S1流面是回轉(zhuǎn)面(見圖1);
(4)平分葉片流道中流量的平均流面(即S2m流面)的形狀與流面的幾何中分面相近。
3計算的數(shù)學模型
有了以上基本假設以后,可得出求解的基本方程[1,2]:
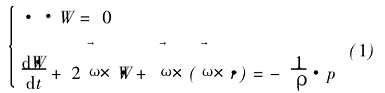
由基本方程(1)通過流線曲率法[4]、有限差分法[7]或有限元法[7]求出S2m流面上的流動參數(shù)分布。計算出S2m流面上的流動參數(shù)分布以后,用S2m流面上的流動參數(shù)求解流場中其他部分的流動參數(shù)。
在S1流面上的準正交線q =θ上的兩點A和B的參數(shù)之間有如下關系:
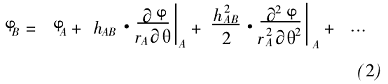
式中,φ―――空間點上的流動參數(shù);
hAB―――點A和B之間沿θ的弧長;
rA―――點A的半徑。
3.1z =常數(shù)時的計算方程式
在z =常數(shù)處,連續(xù)性方程為:
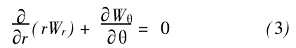
無旋條件為:
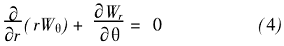
S1流面的方程為r= r(θ,z),該方程在z=常數(shù)時可寫為
S(r,θ) =0 (5)
于是可得
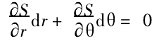
令
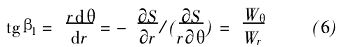
參數(shù)φ沿半徑r的變化為
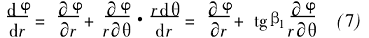
式(6)、(7)代入式(3)、(4)得
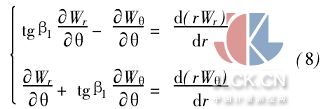
由式(8)得到一階偏導數(shù)
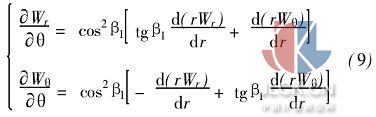
式(9)求導可得二階偏導數(shù)
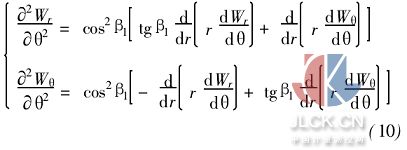
如有必要,可依此類推得到三階、四階等高階偏導數(shù)。
3.2r =常數(shù)時的計算方程式
同理可得在r =常數(shù)處的一階偏導數(shù)和二階偏導數(shù)

如有必要,可依此類推得到三階、四階等高階偏導數(shù)。
4計算步驟
(1)輸入初始數(shù)據(jù),劃分流道中的計算網(wǎng)格;
(2)由基本方程求出S2m流面上的流動參數(shù)分布;
(3)計算出網(wǎng)格結點上的β1和β2的值;
(4)分別用式(9)、(10)、(11)、(12)計算出網(wǎng)格結點上z=常數(shù)和r =常數(shù)時的一階、二階偏導數(shù)的值,其中所用到的導數(shù)項通過三次樣條插值函數(shù)[5,7]求出;
(5)用式(2)來求解S2m流面上任意一點A附近的zA= zB、rA= rB的B點流動參數(shù)。
5計算實例
現(xiàn)以YB355-2型液力變矩器為實例,計算其流場分布。已知參數(shù):泵輪葉片數(shù)zB=26,循環(huán)圓半徑R=0.16m,泵輪轉(zhuǎn)速n =1200 rpm,泵輪與渦輪轉(zhuǎn)速比I =0.7,泵輪入口相對速度W=5.16m/s。在泵輪流道中取7條準正交線(j=0,1,…,6)和5條流線(i =0,1,…,4)。
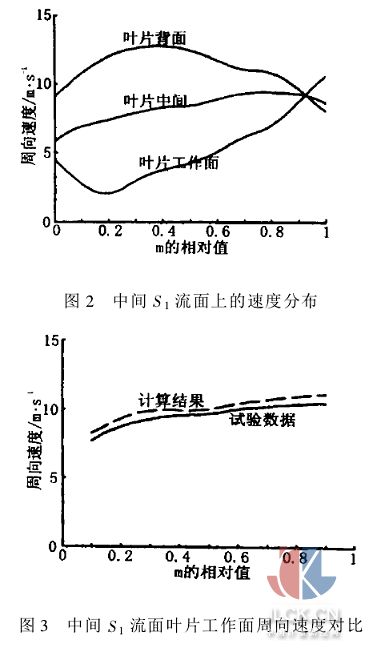
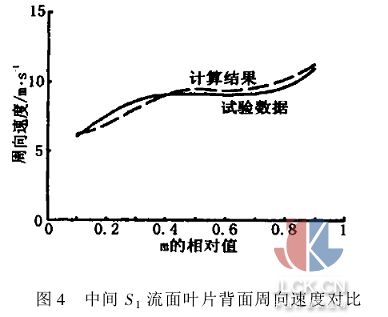
計算結果與試驗數(shù)據(jù)[6]如圖所示。圖2為計算出的中間S1流面上的速度分布,圖3、圖4表示了中間S1流面葉片工作面、背面沿軸面流線方向周向速度的變化。
6結論
(1)通過本文可見,液力變矩器內(nèi)三元流場計算方法的計算結果與實測結果基本吻合,滿足精度要求,且計算過程中不需要迭代,簡便實用。該方法可快速計算出沿周向葉片表面附近的流速及壓力等流動參數(shù)的分布,適用于液力變矩器及其他透平機械內(nèi)流場的實際計算。
(2)造成計算結果與實測結果存在微小差異的原因,主要是在計算過程中進行了大量的數(shù)值微分運算,由此降低了該方法的計算精度所致。但是在一定精度要求的范圍內(nèi),并不影響該方法的應用。
摘自:中國計量測控網(wǎng)







