首頁>技術(shù)中心>技術(shù)資訊>神經(jīng)網(wǎng)絡(luò)技術(shù)在稱重傳感器中的應(yīng)用研究
神經(jīng)網(wǎng)絡(luò)技術(shù)在稱重傳感器中的應(yīng)用研究
發(fā)布時間:2017-09-01
1 引言
現(xiàn)代信息技術(shù)的三大基礎(chǔ)是信息的采集、傳輸和處理技術(shù),即傳感技術(shù)、通信技術(shù)和計算機技術(shù),它們分別構(gòu)成了信息技術(shù)系統(tǒng)的“感官”、“神經(jīng)”和 “大腦”。信息采集系統(tǒng)的首要部件是傳感器,且置于系統(tǒng)的最前端。在一個現(xiàn)代自動檢測系統(tǒng)中,如果沒有傳感器.就無法監(jiān)測與控制表征生產(chǎn)過程中各個環(huán)節(jié)的 各種參量,也就無法實現(xiàn)自動控制。在現(xiàn)代技術(shù)中,傳感器實際上是現(xiàn)代測試技術(shù)和自動化技術(shù)的基礎(chǔ)。
在稱重技術(shù)中,將重物放于稱重系統(tǒng)的承載體上待穩(wěn)定后,就可以準(zhǔn)確地讀出重量值。需要進行快速稱重時,這種傳感器就暴露出缺陷。由于其彈性體的 阻尼比較小,傳感器到達穩(wěn)態(tài)的時間較長,不能滿足快速測量的要求。提高傳感器動態(tài)響應(yīng)的快速性,可從兩方面入手。一是改變其結(jié)構(gòu)、參數(shù)和設(shè)計。減少中間的 傳遞環(huán)節(jié),提高傳感器的固有頻率,從而提高快速性;二是設(shè)計動態(tài)補償器提高動態(tài)響應(yīng)的快速性,即研制基于微處理器的數(shù)字動態(tài)補償裝置,串接在傳感器之后, 以縮短整個測量系統(tǒng)到達穩(wěn)態(tài)的時間。動態(tài)補償器的設(shè)計要基于傳感器的動態(tài)模型。另外通過神經(jīng)網(wǎng)絡(luò)技術(shù)提高傳感器的性能。本文采用神經(jīng)網(wǎng)絡(luò)補償方法,能自動 跟隨傳感器模型的變化,保證稱重系統(tǒng)的快速性。同時給出解決這類問題的幾種其他方案。
2 稱重傳感器的動態(tài)模型
稱重傳感器的動態(tài)模型如圖 1 所示。圖中,K 為彈簧剛度(N?m),C 為阻尼常數(shù)(N/m2),m0為傳感器本身的等效質(zhì)量,G 為被稱重物的重量,B為基座,通常基座的質(zhì)量很大,故認(rèn)為它處于靜止?fàn)顟B(tài)。因為重物與托架之間不是固定聯(lián)接的,所以,需要兩個方程來刻畫上述的稱重傳感器 的動態(tài)特性。
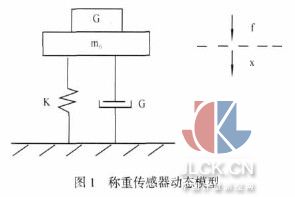
設(shè) m 與 m0之間的作用力為 f,且假定兩者之間無相對運動。
其階躍響應(yīng)如圖 2 所示。動態(tài)過程振蕩周期多,到達穩(wěn)態(tài)的時間長,并且 m 值越大 Td越大,即達到穩(wěn)定的時間越長。必須進行動態(tài)補償,為適應(yīng)被測重量的變化,需要神經(jīng)網(wǎng)絡(luò)自適應(yīng)動態(tài)補償。
3 神經(jīng)網(wǎng)絡(luò)補償器的設(shè)計
若設(shè)計動態(tài)數(shù)字補償器的傳遞函數(shù)是傳感器傳遞函數(shù)的倒數(shù),則整個測量系統(tǒng)的傳遞函數(shù)為 1,具有理想的頻率響應(yīng)特性。根據(jù)這一思想,我們設(shè)計一神經(jīng)網(wǎng)絡(luò)補償器,使整個系統(tǒng)輸出跟蹤系統(tǒng)輸入。
這種多網(wǎng)絡(luò)自學(xué)習(xí)補償結(jié)構(gòu)是由兩個結(jié)構(gòu)和學(xué)習(xí)算法完全相同的神經(jīng)網(wǎng)絡(luò) NN1,NN2 所構(gòu)成。按誤差 E=u- A 減少的方向調(diào)整連接權(quán)并使 u≈A。當(dāng)網(wǎng)絡(luò)收斂后,因網(wǎng)絡(luò) NN1 和 NN2 結(jié)構(gòu)完全相同,所以有 y=u。
對應(yīng)于 m=0.5kg,1.5kg 時的傳遞函數(shù)(8)式和(9)式,采用雙線性變換
s=2(z- 1)/T(z+1),采樣周期取 T=0.02 秒,得離散差分方程為:

采用三層網(wǎng)絡(luò),輸入層有 5 個神經(jīng)元,隱層有8 個神經(jīng)元,輸出層有 1 個神經(jīng)元。采用 BP 算法,其主要思想是對于 q 個輸入樣本:P=[P1,P2,……Pq]已知與其對應(yīng)的輸出樣本為 T=[t11,t2,……,tq]。學(xué)習(xí)的目的是用網(wǎng)絡(luò)的實際輸出 A=[a1,a2,……,aq]與目標(biāo)矢量 t1,t2,……,tq之間的誤差來修改其權(quán)值,使 a1,(l=1,2,……q)與期望的 t1盡可能地接近。隱層的激活函數(shù)為 f1,可調(diào)權(quán)值為W1ij,閾值為 b1i。輸出層的激活函數(shù)為 f2,可調(diào)權(quán)值為 W2i。閾值為 b2i信息的正向傳遞。
因為在線學(xué)習(xí)是有一定時間限制的,而網(wǎng)絡(luò)自身的學(xué)習(xí)也需要耗費一定的時間。如果直接將未訓(xùn)練的神經(jīng)網(wǎng)絡(luò)加入到系統(tǒng)中,當(dāng)誤差變化較大時,很可能 因網(wǎng)絡(luò)自身學(xué)習(xí)的收斂速度跟不上誤差的變化,而影響在線的學(xué)習(xí)效果。要克服直接在線學(xué)習(xí)的這個弱點,可以讓網(wǎng)絡(luò)在線學(xué)習(xí)之前進行離線訓(xùn)練。離線學(xué)習(xí)可以使 神經(jīng)網(wǎng)絡(luò)在系統(tǒng)工作之前預(yù)先完成自身的學(xué)習(xí)過程,以此獲得一個基本反映系統(tǒng)要求的多層網(wǎng)絡(luò),使這個多層網(wǎng)絡(luò)的參數(shù)基本工作在全局最小附近,然后再將這一網(wǎng) 絡(luò)加入系統(tǒng)中去。在系統(tǒng)運行過程中,根據(jù)系統(tǒng)參數(shù)的實時變化,采用在線學(xué)習(xí)算法,讓離線訓(xùn)練過的網(wǎng)絡(luò)再隨系統(tǒng)工作過程中參數(shù)的變化調(diào)整自身參數(shù),從而能快 速、準(zhǔn)確的辨識對象特性。這種離線學(xué)習(xí)與在線學(xué)習(xí)結(jié)合的方法,能很好的發(fā)揮各自的優(yōu)勢,大大提高了神經(jīng)網(wǎng)絡(luò)辨識系統(tǒng)的能力。還可以采用提高學(xué)習(xí)速率或采用 自適應(yīng)速率來加以改進。在滿足精度的前提下,應(yīng)盡量減少結(jié)點數(shù),提高訓(xùn)練速度。上述方法都有利于稱重系統(tǒng)提高快速性和降低抖振。
神經(jīng)網(wǎng)絡(luò) NN2 的結(jié)構(gòu)與算法和 NN1 完全相同,略去。
采用隨機初始化,取采樣周期為 T=0.02 秒,訓(xùn)練矢量是 200 個,達到誤差平方和小于 0.02 或最大循環(huán)次數(shù)為 5000 次。圖 5 表示將訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)加入系統(tǒng)中,當(dāng)參考輸入為:r(k)=0.5 或 r(k)=1.5 時系統(tǒng)的動態(tài)響應(yīng)曲線。
補償?shù)膭討B(tài)過程對比圖 2 可看出未加神經(jīng)網(wǎng)絡(luò)補償?shù)南到y(tǒng)動態(tài)過程有近 100%的超調(diào)量,且動態(tài)調(diào)整時間長約 2 秒。加神經(jīng)網(wǎng)絡(luò)補償后最大超調(diào)量小于 20%,動態(tài)調(diào)整時間縮短為只有 0.2 秒,且適合傳感器參數(shù)變化的情況,該系統(tǒng)適合于快速測量。
自動控制以及計算機控制技術(shù)在解決稱重傳感器的動態(tài)性能方面有廣闊的應(yīng)用價值。實驗仿真表明,自適應(yīng)補償也具有良好的效果。數(shù)字控制器設(shè)計中的 最少拍無差設(shè)計、最少拍無波紋設(shè)計在解決上述問題也有很大的優(yōu)勢,特別是最少拍和無波紋設(shè)計可以減小整個系統(tǒng)的超調(diào)量,具體的仿真結(jié)果我會在后續(xù)的文章中 提出。
4 遺傳神經(jīng)網(wǎng)絡(luò)提高傳感器性能的工作原理
下面以壓阻式壓力傳感器為例,說明遺傳神經(jīng)網(wǎng)絡(luò)在改善傳感器性能中的應(yīng)用。壓阻式壓力傳感器受工作電流波動的影響,那么輸出的電壓值 U就是壓力 P 和工作電流 I 的多元函數(shù),即 U=f (P,)I。也可以認(rèn)為壓阻式壓力傳感器所測得的壓力 P是電壓 U 和工作電流 I 的多元函數(shù),即 P=f (U,)I。要使神經(jīng)網(wǎng)絡(luò)有解決問題的能力,就要用大量的具有普遍性和代表性的學(xué)習(xí)樣本訓(xùn)練網(wǎng)絡(luò),得到網(wǎng)絡(luò)理想的權(quán)值,才能解決實際問題。所以首先要應(yīng)對 壓阻式壓力傳感器進行標(biāo)定實驗,以得到大范圍內(nèi)的學(xué)習(xí)樣本和測試樣本。
4.1 標(biāo)定實驗
標(biāo)定實驗的框圖如圖 6 所示,壓阻式壓力傳感器的標(biāo)準(zhǔn)輸入壓力 P 由砝碼產(chǎn)生,壓阻式壓力傳感器的輸入范圍為 0.1~0.6MPa,可調(diào)電阻改變電路中的工作電流 I,壓阻式壓力傳感器的輸出電壓經(jīng)過調(diào)理電路和數(shù)采卡輸入計算機,由Labwindows/CVI 編制的虛擬電壓表讀取電壓值 U,由電流表讀取電路工作電流值 I,由砝碼讀取標(biāo)定壓力值 P。
4.2 建立、計算數(shù)據(jù)樣本
標(biāo)定實驗所得的標(biāo)定數(shù)據(jù)如表 1 所示,工作電流從 3mA 變化到 7mA。可以看出,同一標(biāo)定壓力下,由于工作電流的影響,壓阻式壓力傳感器的輸出電壓波動很大。
其中:α 為傳感器系統(tǒng)輸出電壓相對波動率;max|ΔU|為最大絕對波動值;UFS為傳感器系統(tǒng)滿量程輸出電壓。
依照表 1 數(shù)據(jù),max|ΔU|=4.7356-2.1048V,故 α=55%,由此可見該傳感器的輸出波動是相當(dāng)大的。
將 0.1,0.3,0.5,0.6MPa 壓力下的工作電流和傳感器輸出電壓作為學(xué)習(xí)樣本,標(biāo)準(zhǔn)壓力值作為學(xué)習(xí)樣本的期望輸出。將 0.2 和 0.4MPa 壓力下工作電流和傳感器輸出電壓作為測試樣本輸入遺傳神經(jīng)網(wǎng)絡(luò)進行計算,得到的測試樣本網(wǎng)絡(luò)輸出如表 2所示。可以看出被測壓力融合值的相對波動情況為:
其中:αP為傳感器系統(tǒng)被測壓力相對波動率;max|ΔP|為被測壓力最大絕對波動值;PFS為傳感器系統(tǒng)被測壓力滿量程值。
根據(jù)表 2 的數(shù)據(jù)得αp=5.7%,傳感器系統(tǒng)的穩(wěn)定性大大提高。
5 結(jié)論
提出了幾種快速稱重方法和提高傳感器性能的原理,著重闡述了基于神經(jīng)網(wǎng)絡(luò)理論,設(shè)計出稱重傳感器神經(jīng)網(wǎng)絡(luò)動態(tài)補償器和提高傳感器性能。仿真研究 表明有效的提高了傳感器動態(tài)響應(yīng)的快速性,且對系統(tǒng)參數(shù)變化具有魯棒性。將先進控制理論應(yīng)用于實際傳感器系統(tǒng)中,為提高傳感器性能開辟了新途徑,促進了稱 重傳感器行業(yè)的發(fā)展。
摘自:中國計量測控網(wǎng)







