數字相機在工業零件檢測中的應用
發布時間:2017-09-01
引言
隨著工業技術的迅速發展,企業對產品質量和生產效率有了更高的要求,高精度在線測控儀器充斥到生產的各個環節,不僅有效地保證了產品質量,提高了生產效率,同時,也避免了加工中由于質量問題引起的浪費現象。
近景攝影測量應用于各種高精度三維測量與大比例尺工程測量及變形監測、工業檢測等領域已有了不少成功的經驗。例如英國將近景攝影測量應用于文物保護,美國俄亥俄州立大學將近景攝影測量應用于移動測圖系統(MMS)等,國內也有不少用于變形監測及防災減災等領域的實例。
本文將介紹應用數字相機與數字圖像處理技術檢測工業零件加工質量的一種方法,但由于多數數字相機是非量測用相機,所以必須對其進行畸變改正。通過對某廠加工的高精度鋼板進行了檢測試驗,證明該方法行之有效。
1目標影像初定位
應用數字圖像處理技術檢測工業零件加工質量的關鍵問題在于準確確定待檢測目標的位置。這一過程一般應在該目標周圍一個較小的范圍內進行,這樣可提高解算速度和減少錯誤發生的概率。為此,首先應用仿射變換模型確定所有待檢測目標在鋼板上的大致位置。仿射變換公式如下:
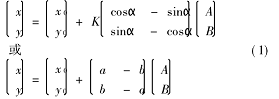
式中x0、y0為平移參數、A為旋轉參數、K為比例參數,a=K×cos (A)、b=K×sin (A)(參見圖1)。
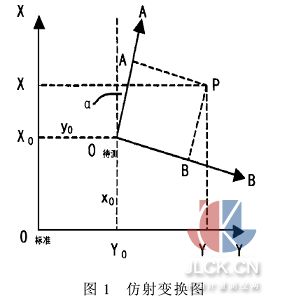
從標準模板與待檢測零件影像中分別量測N(N≥3,最好取4到9個)個均勻分布的同名點,按仿射變換公式計算從標準模板到影像上各目標點的轉換參數,這樣就確定了各目標在影像上的大致位置。
由于數字影像可能存在較大變形,而且一般工業零件影像的特征很少,大部分區域為同一灰度的均勻分布,所以不能用整體匹配的方法確定待檢測目標的坐標。為了給進一步精確定位做準備,需按一般模板匹配的方法對所有目標進行初步配準,即計算目標影像上一定區域內的影像灰度與標準目標模板的信噪比(SNR):
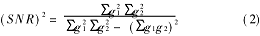
取信噪比最大的點作為待定目標在數字影像上的位置。這實際上只考慮了數字影像的灰度線性畸變,即g1+n1=h0+h1g2+n2。其中h0、h1為灰度線性畸變參數。這時每個目標點的位置應有整像素的精度。
由于最小二乘影像匹配法需要比較精確的點位坐標初值,因此可先用影像特征定位算子提取待定目標的坐標作為最小二乘影像匹配的初值。本文應用Wong-Trinder圓點定位算子提取了圓孔影像的圓心坐標。該算子是通過計算圓形目標的灰度重心提取其圓心坐標的。
以初配準求得的近似位置為中心的比標準圓孔稍大的范圍作為搜索區。先利用閥值T= (最小灰度值+平均灰度值)/2,將搜索窗口中的影像二值化為gij(i= 0,1,…,n- 1;j= 0,1,…m- 1)。
為了防止將其它灰度均勻的區域錯誤地搜索為圓形目標,可根據影像的特征先濾去這些區域。例如本文中的數字影像中圓孔為黑色(灰度值為0),其它區域稍亮,經二值化后為白色(灰度值為255)。因此理想的圓孔目標區域的灰度值總和應為0。但由于存在輻射畸變與幾何畸變,目標區域不會很規則,因此考慮平移一個像素的誤差,目標區域的灰度值總和應小于H= 255×P×R(圓孔的半周長)。凡灰度值總和大于H的區域可以忽略不考慮。
在滿足灰度值總和小于H的區域內逐像素移動,按2.1式計算以每個像素為圓心的標準圓孔模板大小范圍內的灰度重心:
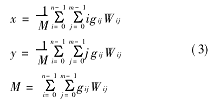
其中Wij是原始圖像上對應像素的灰度值。求得灰度重心后按下式計算這個區域的圓度C:

以圓度C最大的點作為圓心的最終位置。該算子在理想情況下定位精度可達0.01像素。
3最小二乘匹配
最小二乘影像匹配法充分利用影像窗口內的信息進行平差計算,使影像匹配可達到1/10甚至1/100像素的高精度。
最小二乘影像匹配以“灰度差的平方和為最小”作為影像匹配的測度。對于一個影像對g1(x,y)與g2(x,y),如果我們認為影像灰度只存在偶然誤差(隨機噪聲n),即
n1+g1(x,y) =n2+g2(x,y)
或(5)
v=g1(x,y) -g2(x,y)
則最小二乘影像匹配可表示為
2vv=min(6)
一般,最小二乘影像匹配同時考慮數字影像的線性輻射畸變與一次正形幾何畸變,即設x2=a0+a1x+a2y,y2=b0+b1x+b2y,g2=h0+h1g1。其中a0、a1、a2、b0、b1、b2為數字影像的幾何畸變參數,h0、h1為輻射畸變參數。于是最小二乘影像匹配模型轉化為:
g1(x,y) +n1(x,y) =h0+h1g2(a0+a1x+a2y,b0+b1x+b2y) +n2(x,y) (7)
將上式線性化后即得到最小二乘影像匹配的誤差方程式:
v=c1dh0+c2dh1+c3da0+c4da1+c5da2+c6db0+c7db1+c8db2+g2(x,y) -g1(x,y) (8)
式中dh0、dh1、da0、da1、da2、db0、db1、db2是變形參數的改正值,c1…c8是誤差方程式的系數。
列出所有點的誤差方程后按迭代求解的方法解出各變形參數,再由變形參數計算出目標點在影像上的精確位置。這一過程是在Wong-Trinder圓點定位算子求得的目標點周圍的一個小范圍內進行的。
求得所有圓心的準確位置后,與標準模板的圓心位置比較以判斷其加工精度。
4畸變差改正
由于用非量測用數字相機拍攝得到的數字影像不可避免地存在較大畸變,因此按照數字相機的鏡頭畸變模型對數字影像進行畸變差改正是必要的。直接線性變換(DLT)算法即不需要在影像上有框標,也不需要有攝影機內外方位參數的起始近似值。特別適合于對非量測相機攝取的影像的歸化。用于量測用相機拍攝的影像也具有顯著優點。
直接線性變換的基本公式為
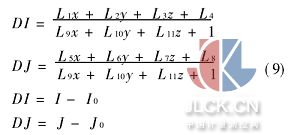
其中x、y為物方坐標,I、J為數字化的影像坐標,I0、J0為數字影像對應于托架上的光學影像的原點坐標,L1,…L11是轉換后的影像坐標和相片坐標之間的變換參數。當應用于二維情況時,上式簡化為:
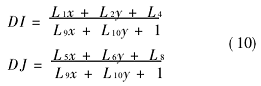
9式與10式沒有考慮影像的畸變。數字相機的誤差來源主要有:數字化影像變形、鏡頭畸變和CCD陣列的線性位移。
CCD陣列的鏡頭畸變(Di,Dj)可寫為:

這里Dri,Drj表示鏡頭x,y方向的徑向畸變,Ddi,Ddj表示離心畸變,Dm是掃描方向的線性位移。
一般,鏡頭的徑向畸變可以寫為:
Dr=k1r3+k2r5+k3r7(12)
式中k1,k2,k3是徑向畸變系數,r是像點輻射距: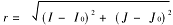
于是,x、y方向的徑向畸變可以表示為:
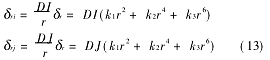
離心畸變可以表示為:
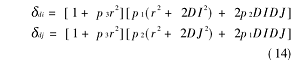
其中p1,p2,p3表示離心畸變的改正系數。
對于CCD陣列的線性變形一般用一個多項式逼近:
Dm=m1l+m2l3+m3l5+m4l7(15)
這樣就得到了與10式相對應的考慮畸變的嚴密檢校數學模型:
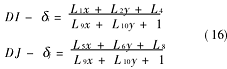
通常稱L1,…L11為直接線性變換參數,k1,k2,k3,p1,p2,p3,m1,m2,m3,m4為變換改正參數。
直接線性變換參數與變形改正參數之間存在密切的相關性,需采用序貫平差算法迭代求解兩類參數。
直接線性變換的參數方程16式可寫為
DI-Di=A/C
DJ-Dj=B/C(17)
其中A=L1x+L2y+L4,B=L5x+L6y+L8,C=L9x+L10y+ 1。
用矩陣形式表示為:
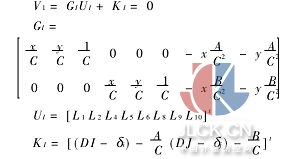
同樣,由16式可得到變形改正參數的觀測方程:
I-A/C=I0+Drj+Ddj+Dm
J-B/C=J0+Drj+Ddj(19)
相應的矩陣形式為:
Vd=GdUd+Kd= 0
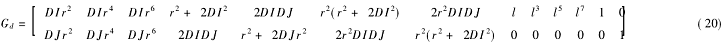
反復迭代計算上述兩類誤差方程,直到直接線性變換參數與畸變改正參數的改正值都小于限差為止,即可獲得兩類參數的正確解,進而對原始影像加以改正。
5試驗結果
根據以上討論的方法,在Visual C++6.0環境下編程對某廠加工的高精度鋼板進行了檢測試驗。圖2是用數字相機拍攝的鋼板的數字影像:
鋼板概略尺寸為505m×316mm,其中圓孔106個,半徑分別為4.5mm和3.6mm,矩形孔76個。數字影像幅面為1280×1024像素,攝影比例尺為0.4309mm/pixel。要求檢測圓孔的位置與大小是否符合設計要求。

目前,該廠主要通過人工量測獲得圓孔在鋼板上的位置。由于精度要求高,人工量測一塊鋼板一般需要7~8個小時,而且很容易出錯。而用數字圖像識別方法檢測同一鋼板僅需要幾秒鐘至幾分鐘時間。效益十分可觀。
在該試驗中,只考慮了x、y二維坐標,但在實際工業零件檢測中一般需要考慮三維坐標。試驗所得數據如下:
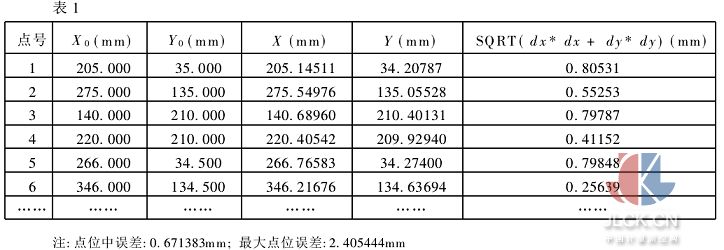
表1列出了利用Wong-Trinder圓點定位算子求得的圓心位置與設計坐標相比較的精度結果。
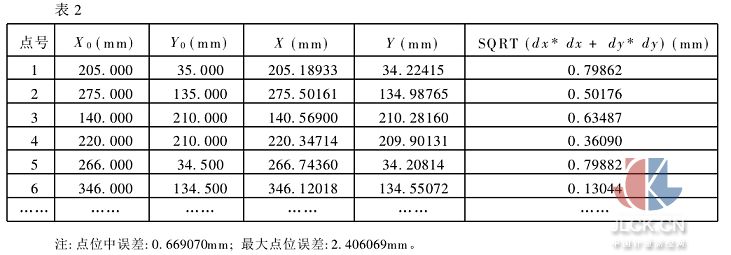
表2列出了利用最小二乘影像匹配法求得的圓心位置與設計坐標相比較的精度結果。
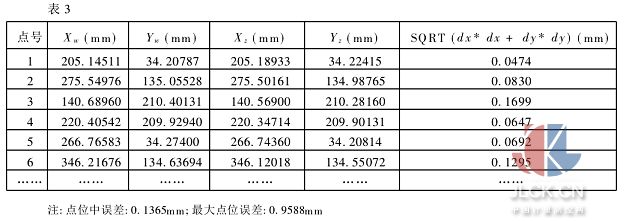
表3列出了利用最小二乘匹配法求得的圓心位置與利用Wong-Trinder圓點定位算子求得圓心位置與設計坐標相比較的精度情況。
可見利用Wong-Trinder圓點定位算子求得的圓心位置已相當準確,與利用最小二乘影像匹配法求得的圓心位置結果精度相當,而且提取出的圓心位置結果可靠。
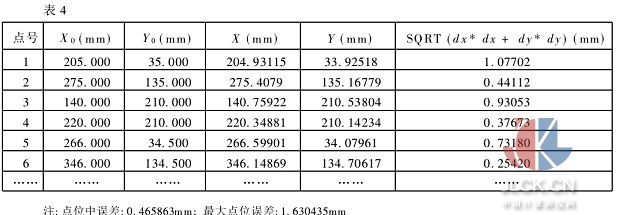
表4列出了經過直接線性變換改正后的圓心位置與設計坐標相比較的情況。
可見圓心定位精度明顯提高。認為經過畸變改正后影像的剩余畸變很小,即與實際鋼板相符,所以求得的點位誤差主要為加工誤差。
6結論
(1)盡管試驗用的數字相機為非量測用相機,但已達到了相當的精度。Wong-Trinder圓點定位算子求得的圓心位置與最小二乘匹配法求得的圓心位置比較,點位中誤差只有0.1365mm,最大點位誤差僅為0.9588mm。證明用非量測用數字相機與數字圖像處理技術進行工業零件檢測是可行的。應用在線數據(圖像)獲取和實時圖像處理技術,可以大大提高生產效率,降低生產成本。
(2)實際應用的關鍵在于要有加工精確的標準模板作為影像匹配的基準或提供精確的控制點。
(3)要有合理的相機鏡頭畸變改正模型。
摘自:中國計量測控網







